题目内容
设函数
，给出下列四个命题：
①
时，
是奇函数 ②
时，方程
只有一个实根
③的图象关于点
对称 ④方程至多两个实根
其中正确的命题是（ ）
A.①④ B．①③ C．①②③ D．①②④
【答案】
C
【解析】对于①，若f（x）是奇函数，则f（-x）=-x|x|-bx+c=-f（x）对任意x∈R恒成立，可得c=0，故①正确；对于②，b=0时，得f（x）=x|x|+c在R上为单调增函数，且值域为R，所以方程f（x）=0有且只有一个实根，故②正确；对于③，因为f（-x）=-x|x|-bx+c，所以f（-x）+f（x）=2c，可得函数f（x）的图象关于点（0，c）对称，故③正确；对于④，当b=1，c=0时，f（x）=x|x|+x在R上为增函数，此时方程f（x）=0有且只有一个实根，故④错．故答案为：①②③
练习册系列答案
相关题目
，给出下列四个命题：①
时，
是奇函数②
，时，方程
只有一个实根③
对称④方程
，给出下列四个命题：
时，
是奇函数 ②
时，方程
只有一个实根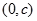
对称 ④方程
，给出下列四个命题：
时，
是奇函数；
时，方程
只有一个实根；
对称；
，给出下列四个命题：
时，函数
是单调函数；
时，方程
只有一个实根
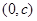对称；