题目内容
已知函数f(x)=|
-3|,x∈(0,+∞)
(1)画出y=f(x)的大致图象,并根据图象写出函数y=f(x)的单调区间;
(2)设0<a<
,b>
试比较f(a),f(b)的大小.
(3)是否存在实数a,b,使得函数y=f(x)在[a,b]上的值域也是[a,b]?若存在,求出a,b的值,若不存在,说明理由.
| 1 |
| x |
(1)画出y=f(x)的大致图象,并根据图象写出函数y=f(x)的单调区间;
(2)设0<a<
| 1 |
| 9 |
| 1 |
| 3 |
(3)是否存在实数a,b,使得函数y=f(x)在[a,b]上的值域也是[a,b]?若存在,求出a,b的值,若不存在,说明理由.
分析:(1)由y=
,x∈(0,+∞)的图象向下平移3个单位,再把x轴下方的翻折到x轴上方,可得y=f(x)的大致图象,从而可得函数y=f(x)的单调区间;
(2)分别表示出f(a),f(b),确定其范围,即可比较f(a),f(b)的大小;
(3)可假设存在实数a,b,使得y=f(x)的定义域和值域都是[a,b],由此出发探究a,b的可能取值,可分三类:a,b∈(0,
)时,a,b∈(
,+∞)时,a∈(0,
),b∈(
,+∞),分别建立方程,寻求a,b的可能取值,若能求出这样的实数,则说明存在,否则说明不存在.
| 1 |
| x |
(2)分别表示出f(a),f(b),确定其范围,即可比较f(a),f(b)的大小;
(3)可假设存在实数a,b,使得y=f(x)的定义域和值域都是[a,b],由此出发探究a,b的可能取值,可分三类:a,b∈(0,
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答: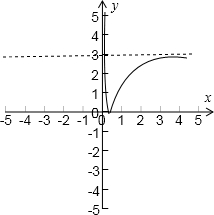 解:(1)由y=
解:(1)由y=
,x∈(0,+∞)的图象向下平移3个单位,再把x轴下方的翻折到x轴上方,可得y=f(x)的大致图象
如图所示
函数y=f(x)的单调减区间为(0,
),单调增区间为(
,+∞);
(2)由题意,f(a)=
-3,f(b)=3-
∵0<a<
,b>
∴
>9,0<
<3
∴f(a)>6,0<f(b)<3
∴f(a)>f(b);
(3)不存在实数a,b满足条件.
假设存在实数a,b,使得y=f(x)的定义域和值域都是[a,b],而y≥0,x≠0,所以应有a>0
又f(x)=
①当a,b∈(0,
)时,函数在(0,
)上为减函数,
故有
,即
,由此可得a=b,此时实数a,b的值不存在.
②当a,b∈(
,+∞)时,函数在(
,+∞)上为增函数,
故有
,即
,由此可得a,b是方程x2+3x-1=0的根,所以x=
,不合题意,故此时实数a,b也不存在.
③当a∈(0,
),b∈(
,+∞)时,显然
∈[a,b],而f(
)=0∈[a,b]不可能,此时a,b也不存在
综上可知,适合条件的实数a,b不存在.
 解:(1)由y=
解:(1)由y=| 1 |
| x |
如图所示
函数y=f(x)的单调减区间为(0,
| 1 |
| 3 |
| 1 |
| 3 |
(2)由题意,f(a)=
| 1 |
| a |
| 1 |
| b |
∵0<a<
| 1 |
| 9 |
| 1 |
| 3 |
∴
| 1 |
| a |
| 1 |
| b |
∴f(a)>6,0<f(b)<3
∴f(a)>f(b);
(3)不存在实数a,b满足条件.
假设存在实数a,b,使得y=f(x)的定义域和值域都是[a,b],而y≥0,x≠0,所以应有a>0
又f(x)=
|
①当a,b∈(0,
| 1 |
| 3 |
| 1 |
| 3 |
故有
|
|
②当a,b∈(
| 1 |
| 3 |
| 1 |
| 3 |
故有
|
|
-3±
| ||
| 2 |
③当a∈(0,
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
综上可知,适合条件的实数a,b不存在.
点评:本题考查函数的图象,考查函数与方程的综合应用,考查绝对值函数,二次方程根与系数的关系等,解题的关键是理解题意,将问题正确转化,进行分类讨论探究,是一道综合性较强的题,思维难度大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|