题目内容
已知命题p:函数 的图象关于原点对称;q:幂函数恒过定点(1,1).则( )
的图象关于原点对称;q:幂函数恒过定点(1,1).则( )A.p∨q为假命题
B.(¬p)∨q为真命题
C.p∧(¬q)为真命题
D.(¬p)∧(¬q)为真命题
【答案】分析:由于y=sin(x+ )=cosx为偶函数,故命题p假,而命题q真,利用复合命题的真值表可得答案.
)=cosx为偶函数,故命题p假,而命题q真,利用复合命题的真值表可得答案.
解答:解:∵y=sin(x+ )=cosx为偶函数,其图象关于y轴对称,不关于原点对称,故命题p假;
)=cosx为偶函数,其图象关于y轴对称,不关于原点对称,故命题p假;
而命题q:幂函数y=xα恒过定点(1,1),是真命题;
∴¬p真,¬q假,
∴p∨q真,A错;(¬p)∨q为真,正确;p∧(¬q)为假,C错;(¬p)∧(¬q)为假.
故选B.
点评:本题考查复合命题的真假,根据题意判断出p假q真是关键,着重考查复合命题的真值表,属于中档题.
 )=cosx为偶函数,故命题p假,而命题q真,利用复合命题的真值表可得答案.
)=cosx为偶函数,故命题p假,而命题q真,利用复合命题的真值表可得答案.解答:解:∵y=sin(x+
 )=cosx为偶函数,其图象关于y轴对称,不关于原点对称,故命题p假;
)=cosx为偶函数,其图象关于y轴对称,不关于原点对称,故命题p假;而命题q:幂函数y=xα恒过定点(1,1),是真命题;
∴¬p真,¬q假,
∴p∨q真,A错;(¬p)∨q为真,正确;p∧(¬q)为假,C错;(¬p)∧(¬q)为假.
故选B.
点评:本题考查复合命题的真假,根据题意判断出p假q真是关键,着重考查复合命题的真值表,属于中档题.

练习册系列答案
相关题目
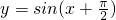 的图象关于原点对称;q:幂函数恒过定点(1,1).则
的图象关于原点对称;q:幂函数恒过定点(1,1).则 的图象与x轴有交点,命题q:f(x)=(2a-1)x为R上的减函数,则p是q的( )条件.
的图象与x轴有交点,命题q:f(x)=(2a-1)x为R上的减函数,则p是q的( )条件. 的图象关于原点对称;q:幂函数恒过定点(1,1).则( )
的图象关于原点对称;q:幂函数恒过定点(1,1).则( ) 的图象过定点(-1,1);命题q:如果函数
的图象过定点(-1,1);命题q:如果函数 的图象关于原点对称,则函数
的图象关于原点对称,则函数 关于(3,0)点对称,则( )
关于(3,0)点对称,则( )