题目内容
已知命题p：函数
的图象与x轴有交点，命题q：f（x）=（2a-1）x为R上的减函数，则p是q的（ ）条件．A．充分不必要
B．必要不充分
C．充要
D．既不充分也不必要
【答案】分析：易得p，q对应的集合分别为：{a|a≤2}和{a|
}，由集合的包含关系可得答案．
解答：解：由函数
的图象与x轴有交点可得，
△=
，解得a≤2；
又因为f（x）=（2a-1）x为R上的减函数，
所以0＜2a-1＜1，解得
，
因为集合{a|a≤2}真包含集合{a|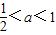
}，
所以p是q的必要不充分条件，
故选B
点评：本题考查充要条件的判断，转化为集合间的包含关系是解决问题的关键，属基础题．
}，由集合的包含关系可得答案．解答：解：由函数
的图象与x轴有交点可得，△=
，解得a≤2；又因为f（x）=（2a-1）x为R上的减函数，
所以0＜2a-1＜1，解得
，因为集合{a|a≤2}真包含集合{a|
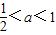}，所以p是q的必要不充分条件，
故选B
点评：本题考查充要条件的判断，转化为集合间的包含关系是解决问题的关键，属基础题．
练习册系列答案
相关题目
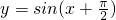的图象关于原点对称；q：幂函数恒过定点（1，1）．则
的图象关于原点对称；q：幂函数恒过定点（1，1）．则（ ）
的图象关于原点对称；q：幂函数恒过定点（1，1）．则（ ）
的图象过定点(－1,1)；命题q：如果函数
的图象关于原点对称，则函数
关于(3,0)点对称，则（ ）