Question

已知函数f(x)=

(x+2)2，x＜0 4，          x=0 (x-2) 2，x＞0.

（1）画出f（x）的草图并指出单调区间；
（2）若f（x）=16，求相应x的值．

Answer 1

分析：（1）分段即可作出f（x）的草图，根据图象可得函数的单调区间；
（2）结合图象分两种情况：x＜-2，x＞2解方程f（x）=16即可；

解答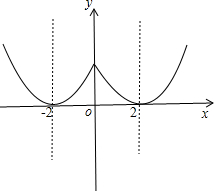：解：（1）函数f（x）的草图如下所示：
f（x）的单调增区间为[-2，0），（2，+∞），单调减区间为（-∞，-2），（0，2]．
（2）由f（x）=16，得（x+2）²=16，解得x=2（舍）或-6；
或（x-2）²=16，解得x=6或-2（舍），
所以x的值为6或-6．

点评：本题考查函数图象的作法、函数单调区间的求解，属基础题．