题目内容
已知不等式|1-kxy|>|kx-y|.
(1)当k=1,y=2时,解关于x的不等式|1-kxy|>|kx-y|;
(2)若不等式|1-kxy|>|kx-y|对任意满足|x|<1,|y|<1的实数x,y恒成立,求实数k的取值范围
(1)当k=1,y=2时,解关于x的不等式|1-kxy|>|kx-y|;
(2)若不等式|1-kxy|>|kx-y|对任意满足|x|<1,|y|<1的实数x,y恒成立,求实数k的取值范围
(1) x∈(-∞,-1) ∩(1,+ ∞).
(2) k∈[-1,1]
(1)当k=1,y=2时,不等式|1-kxy|>|kx-y|即为|1-2x|>|x-2|.
所以1-4x+4x2>x2-4x+4 x2>1,所以x∈(-∞,-1) ∩(1,+ ∞). (5分)
x2>1,所以x∈(-∞,-1) ∩(1,+ ∞). (5分)
(2)由已知得|1-kxy|>|kx-y| |1-kxy|2>|kx-y|2
|1-kxy|2>|kx-y|2 1+k2x2y2>k2x2+y2,
1+k2x2y2>k2x2+y2,
即(k2x2-1)(y2-1) >0对任意满足|x|<1,|y|<1的实数x,y恒成立.
而y2<1,所以y2-1<0,故(k2x2-1)(y2-1) >0 k2x2-1<0.
k2x2-1<0.
于是命题转化为k2x2-1<0对任意满足|x|<1的实数x恒成立. (8 分)
分)
当x=0时,易得k∈R;
当x≠0时,有k2<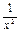 对任意满足|x|<1,x≠0的实数x恒成立.
对任意满足|x|<1,x≠0的实数x恒成立.
由0<|x|<1 0<x2<1
0<x2<1
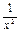 ∈(1,+ ∞),所以k2≤1.
∈(1,+ ∞),所以k2≤1.
综合以上得k∈[-1,1]即为所求的取值范围.
所以1-4x+4x2>x2-4x+4
 x2>1,所以x∈(-∞,-1) ∩(1,+ ∞). (5分)
x2>1,所以x∈(-∞,-1) ∩(1,+ ∞). (5分)(2)由已知得|1-kxy|>|kx-y|
 |1-kxy|2>|kx-y|2
|1-kxy|2>|kx-y|2 1+k2x2y2>k2x2+y2,
1+k2x2y2>k2x2+y2,即(k2x2-1)(y2-1) >0对任意满足|x|<1,|y|<1的实数x,y恒成立.
而y2<1,所以y2-1<0,故(k2x2-1)(y2-1) >0
 k2x2-1<0.
k2x2-1<0.于是命题转化为k2x2-1<0对任意满足|x|<1的实数x恒成立. (8
 分)
分) 当x=0时,易得k∈R;
当x≠0时,有k2<
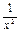 对任意满足|x|<1,x≠0的实数x恒成立.
对任意满足|x|<1,x≠0的实数x恒成立.由0<|x|<1
 0<x2<1
0<x2<1
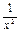 ∈(1,+ ∞),所以k2≤1.
∈(1,+ ∞),所以k2≤1.综合以上得k∈[-1,1]即为所求的取值范围.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 的解集是
的解集是 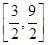

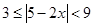 的解集为( )
的解集为( )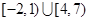
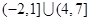
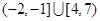
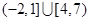
 .
. 的解集;
的解集; ,
, 恒成立,求实数
恒成立,求实数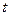 的取值范围.
的取值范围. 的解集为M,不等式
的解集为M,不等式 的解集为N,则M∩N=
的解集为N,则M∩N=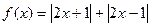 ,
,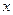 有
有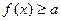 成立,求
成立,求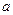 的取值范围;
的取值范围;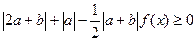 ,对于任意的
,对于任意的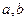 都成立,求
都成立,求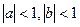 ,求证:
,求证: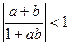 .
.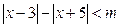 在R上恒成立,则m的取值范围 .
在R上恒成立,则m的取值范围 .