题目内容
（2010•湖北模拟）等边三角形ABC的三个顶点在一个半径为1的球面上，A、B两点间的球面距离为
，则△ABC的外接圆的面积为（ ）
| π |
| 2 |
分析：根据题意得：在△AOB中利用弧长公式，可得∠AOB=
，利用等腰直角三角形求出等边三角形ABC的边长为
，最后用正弦定理求出△ABC的外接圆的半径，最后计算出△ABC的外接圆的面积．
| π |
| 2 |
| 2 |
解答：解：如图，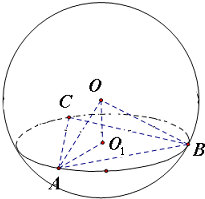
设球心为O，△ABC的外接圆的圆心为O1，连接OA、OB
∵A、B两点间的球面距离为
，球的半径为1
∴∠AOB=
结合Rt△AOB中，OA=OB=1，得
AB=
=
在等边△ABC中，根据正弦定理得：
=2R⇒外接圆的半径为R=
=
∴外接圆的面积为S=πR2=
π
故选C
设球心为O，△ABC的外接圆的圆心为O1，连接OA、OB∵A、B两点间的球面距离为
| π |
| 2 |
∴∠AOB=
| π |
| 2 |
结合Rt△AOB中，OA=OB=1，得
AB=
| AO2+BO2 |
| 2 |
在等边△ABC中，根据正弦定理得：
| AB |
| sin60° |
| AB | ||
|
| ||
| 3 |
∴外接圆的面积为S=πR2=
| 2 |
| 3 |
故选C
点评：本题考查了立体几何中球面距离的概念，以及用正弦定理求三角形的外接圆的半径等等知识，属于中档题，综合的几何知识较多，值得同学们思考．
练习册系列答案
通城学典默写能手系列答案
相关题目
（2010•湖北模拟）如图，正方体AC1的棱长为1，连接AC1，交平面A1BD于H，则以下命题中，错误的命题是（ ）
（2010•湖北模拟）如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，且PA=AB，点E是PD的中点．