题目内容
在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2, ,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
(1) 7.(2) 0.4
解析试题分析:解 (1)∵这6位同学的平均成绩为75分,
∴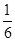 (70+76+72+70+72+x6)=75,
(70+76+72+70+72+x6)=75,
解得x6=90, 3分
这6位同学成绩的方差
s2=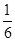 ×[(70-75)2+(76-75)2+(72-75)2+(70-75)2+(72-75)2+(90-75)2]=49,
×[(70-75)2+(76-75)2+(72-75)2+(70-75)2+(72-75)2+(90-75)2]=49,
∴标准差s=7 6分
(2)从前5位同学中,随机地选出2位同学的成绩有:(70,76),(70,72),(70,70),(70,72),(76,72),(76,70),(76,72),(72,70),(72,72),(70,72),共10种, 9分
恰有1位同学成绩在区间(68,75)中的有:(70,76),(76,72),(76,70),(76,72),共4种,所求的概率为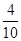 =0.4 11分
=0.4 11分
即恰有1位同学成绩在区间(68,75)中的概率为0.4 12分
考点:方差,古典概型
点评:解决的关键是根据方差的定义得到求解,以及古典概型 概率公式来得到概率值,属于基础题。

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案某种产品的广告费支出 (单位:万元)与销售额
(单位:万元)与销售额 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
广告费支出 | 2 | 4 | 5 | 6 | 8 |
销售额 | 30 | 40 | 60 | 50 | 70 |
 ,
,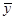 的值并求点
的值并求点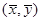 对应的复数
对应的复数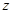 ;
;(2)完成下表并求回归直线方程
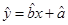 。
。 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
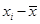 | | | | | |
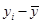 | | | | | |
 | | | | | |
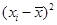 | | | | | |
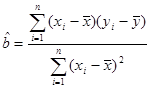 )
) 为了解目前老年人居家养老还是在敬老院养老的意向,共调查了50名老年人,其中男性明确表示去敬老院养老的有5人,女性明确表示居家养老的有10人,已知在全部50人中随机地抽取1人明确表示居家养老的概率为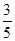 。
。
(1)请根据上述数据建立一个2×2列联表;
(2)居家养老是否与性别有关?请说明理由。
参考公式: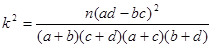
参考数据:
 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(本题满分12分)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
 | 文艺节目 | 新闻节目 | 总计 |
| 20~40岁 | 40 | 18 | 58 |
| 大于40岁 | 15 | 27 | 42 |
| 总计 | 55 | 45 | 100 |
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应抽取几名?
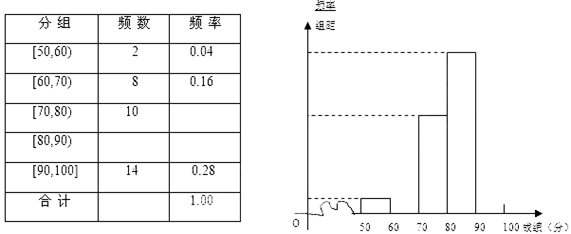
 段的有多少人;
段的有多少人;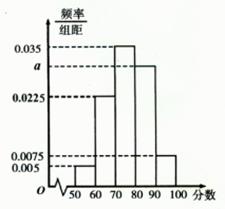
 的值;
的值;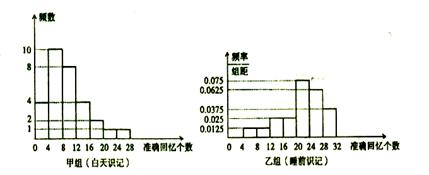


 ,
, 值,并补全频数条形图;
值,并补全频数条形图;