题目内容
设数列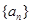 :
: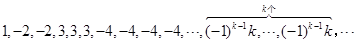 ,即当
,即当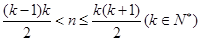 时,记
时,记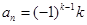 .记
.记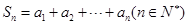 . 对于
. 对于 ,定义集合
,定义集合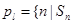 是
是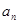 的整数倍,
的整数倍,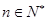 ,且
,且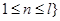 .
.
(1)求集合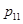 中元素的个数;
中元素的个数;
(2)求集合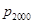 中元素的个数.
中元素的个数.
【答案】
(1)2 (2)1008
【解析】(1)由数列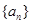 的定义,得
的定义,得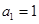 ,
,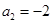 ,
, ,
,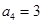 ,
,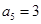 ,
,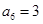 ,
,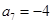 ,
,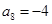 ,
,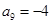 ,
,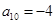 ,
,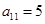 ,∴
,∴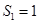 ,
, ,
,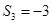 ,
,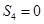 ,
,
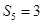 ,
,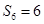 ,
,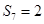 ,
,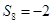
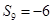 ,
,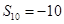 ,
,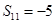 ,
,
∴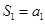 ,
,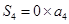 ,
,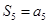 ,
,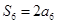 ,
,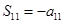 ,
,
∴集合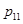 中元素的个数为5.
中元素的个数为5.
(2)先证: ,
,
事实上,①当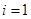 时,
时,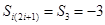 ,
,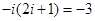 ,原等式成立;
,原等式成立;
②当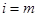 时成立,即
时成立,即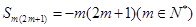 ,
,
则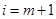 时,
时,
 ,
,
综合①②可得 ,于是,
,于是,
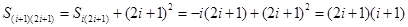 ,
,
由上式可知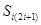 是
是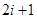 的倍数,而
的倍数,而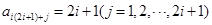 ,
,
∴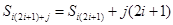 是
是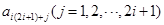 的倍数,
的倍数,
又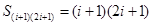 不是
不是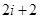 的倍数,
的倍数,
而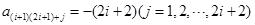 ,
,
∴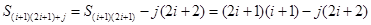 不是
不是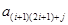
 的倍数,
的倍数,
故当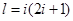 时,集合
时,集合 中元素的个数为
中元素的个数为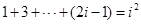 ,
,
于是,当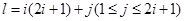 时,集合
时,集合 中元素的个数为
中元素的个数为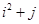 ,
,
又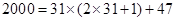 ,故集合
,故集合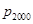 中元素的个数为
中元素的个数为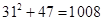 .
.
【考点定位】本小题主要考查集合、数列的概念和运算、计数原理等基础知识,考查探究能力及运用数学归纳法的推理论证能力.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目