题目内容
(Ⅰ)(坐标系与 参数方程)直线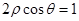 与圆
与圆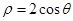 相交的弦长为 .
相交的弦长为 .
(Ⅱ)(不等式选讲)设函数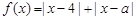
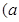 >1),且
>1),且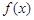 的最小值为
的最小值为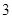 ,若
,若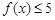 ,则
,则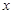 的取值范围
的取值范围
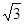 ,3≤x≤8
,3≤x≤8
解析试题分析: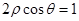 即
即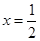 ,
,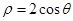 即
即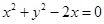 ,配方得,
,配方得, ,
,
所以,直线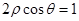 与圆
与圆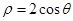 相交的弦长为
相交的弦长为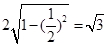 。
。
考点:极坐标方程与普通方程的互化,直线与圆的位置关系。
点评:中档题,极坐标方程化为普通方程,常用的公式有,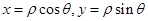 ,
,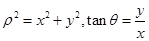 等。涉及圆的弦长问题,利用几何法往往形象直观,易于理解。
等。涉及圆的弦长问题,利用几何法往往形象直观,易于理解。
试题分析:∵函数f(x)=|x-4|+|x-a|≥|x-4+a-x|=|a-4|,f(x)的最小值为3,∴|a-4|=3,
解得,a=1或7,又a>1,∴a=7,
即f(x)=|x-4|+|x-7|≤5,
若x≤4,f(x)=4-x+7-x=11-2x≤5,解得x≥3,故3≤x≤4;
若4<x<7,f(x)=x-4+7-x=3,恒成立,故4<x<7;
若x≥7,f(x)=x-4+x-7=2x-11≤5,解得x≤8,故7≤x≤8;
综上3≤x≤8,
故答案为:3≤x≤8.
考点:绝对值不等式的性质,绝对值的几何意义,绝对值不等式的解法。
点评:中档题,求此类函数的最值问题,可以利用绝对值不等式的性质,也可以利用绝对值的几何意义。解绝对值不等式,通常利用“分段讨论法”,也可以利用绝对值的几何意义。

练习册系列答案
相关题目
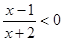 的解集是___________.
的解集是___________.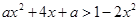 对一切
对一切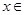 R恒成立,则实数a的取值范围是 .
R恒成立,则实数a的取值范围是 . a2
a2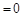 ,a1a42
,a1a42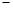 a2
a2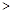 a2
a2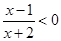 的解集为
的解集为 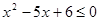 的解集为 。
的解集为 。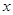 的不等式
的不等式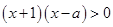 的解集是
的解集是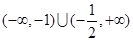 ,则
,则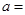 .
.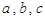 满足
满足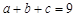 ,
,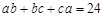 ,则
,则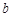 的取值范围是 .
的取值范围是 . 的不等式
的不等式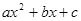 <0的解集是
<0的解集是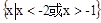 ,则关于
,则关于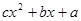 >0的解集是___________.
>0的解集是___________.