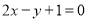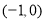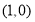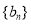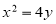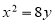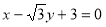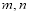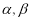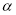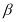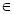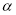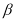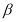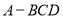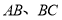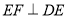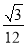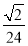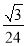题目内容
(1)求圆心在 轴上,且与直线
轴上,且与直线 相切于点
相切于点 的圆的方程;
的圆的方程;
(2)已知圆 过点
过点 ,且与圆
,且与圆 关于直线
关于直线 对称,求圆
对称,求圆 的方程.
的方程.
(1) (2)
(2)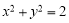
【解析】
试题分析:(1)根据题意可设圆心 ,所以圆心和切点的连线与直线
,所以圆心和切点的连线与直线 垂直,根据斜率相乘等于
垂直,根据斜率相乘等于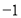 ,可求出圆心坐标,圆心与切点间的距离为半径,即可求出圆的标准方程。(2)两圆关于直线对称即圆心关于直线对称,半径不变。即两圆心的连线被直线
,可求出圆心坐标,圆心与切点间的距离为半径,即可求出圆的标准方程。(2)两圆关于直线对称即圆心关于直线对称,半径不变。即两圆心的连线被直线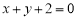 垂直平分,则可求出圆
垂直平分,则可求出圆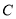 的圆心坐标,根据两点间距离求半径。
的圆心坐标,根据两点间距离求半径。
试题解析:【解析】
(1)根据题意可设圆心 ,则
,则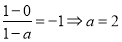 ,即圆心为
,即圆心为 ,半径
,半径 ,则所求圆的方程为
,则所求圆的方程为 . 6分
. 6分
(2)设圆心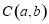 ,
,
∴ 又
又 在圆上所以圆C的方程为
在圆上所以圆C的方程为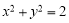 . 12分
. 12分
考点:1求圆的方程;2点关于直线的对称点。

练习册系列答案
相关题目