题目内容
已知函数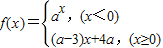 满足对任意的实数x1≠x2都有
满足对任意的实数x1≠x2都有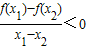 成立,则实数a的取值范围是( )
成立,则实数a的取值范围是( )A.(3,+∞)
B.(0,1)
C.
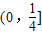
D.(1,3)
【答案】分析:由题意可知,0<a<1,且a-3<0,且4a≤1,解之即得答案.
解答:解:∵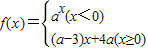 ,对任意的实数x1≠x2都有
,对任意的实数x1≠x2都有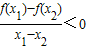 成立,
成立,
∴函数f(x)在定义域内单调递减,令g(x)=ax,依题意,f(0)≤g(0),即4a≤1,
∴ ,解得0<a≤
,解得0<a≤ .
.
∴实数a的取值范围是0<a≤ .
.
故选C.
点评:本题考查函数单调性的性质及其应用,理解“对任意的实数x1≠x2都有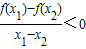 成立?函数f(x)在定义域内单调递减”是关键,也是难点所在,考查解不等式组的能力,属于中档题.
成立?函数f(x)在定义域内单调递减”是关键,也是难点所在,考查解不等式组的能力,属于中档题.
解答:解:∵
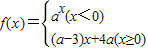 ,对任意的实数x1≠x2都有
,对任意的实数x1≠x2都有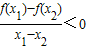 成立,
成立,∴函数f(x)在定义域内单调递减,令g(x)=ax,依题意,f(0)≤g(0),即4a≤1,
∴
 ,解得0<a≤
,解得0<a≤ .
.∴实数a的取值范围是0<a≤
 .
.故选C.
点评:本题考查函数单调性的性质及其应用,理解“对任意的实数x1≠x2都有
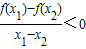 成立?函数f(x)在定义域内单调递减”是关键,也是难点所在,考查解不等式组的能力,属于中档题.
成立?函数f(x)在定义域内单调递减”是关键,也是难点所在,考查解不等式组的能力,属于中档题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
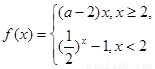 满足对任意的实数
满足对任意的实数 都有
都有 成立,则实数
成立,则实数 的取值范围为( )
的取值范围为( ) B.
B. C.
C. D.
D.
 满足对任意的实数
满足对任意的实数 都有
都有 成立,则实数
成立,则实数 的取值范围为( )
的取值范围为( ) B.
B.
 D.
D.
 满足对任意的
满足对任意的 都有
都有 成立,则
成立,则 = 。
= 。 满足对任意的
满足对任意的 都有
都有 成立,则
成立,则 = 。
= 。