题目内容
某工厂师徒二人各加工相同型号的零件,是否加工出精品均互不影响.已知师傅加工一个零件是精品的概率为
,师徒二人各加工2个零件都是精品的概率为
.
(1)求徒弟加工2个零件都是精品的概率;
(2)若师徒二人各加工这种型号的零件2个,求徒弟加工该零件的精品数多于师傅的概率.
| 2 |
| 3 |
| 1 |
| 9 |
(1)求徒弟加工2个零件都是精品的概率;
(2)若师徒二人各加工这种型号的零件2个,求徒弟加工该零件的精品数多于师傅的概率.
分析:(1)设出徒弟加工1个零件是精品的概率,由相互独立事件同时发生的概率得到关于概率的方程,解方程即可;
(2)写出两个人加工零件对应的是精品的概率,徒弟加工该零件的精品数多于师父包括三种情况,这三种情况是互斥的,根据相互独立事件同时发生的概率和互斥事件的概率得到结果.
(2)写出两个人加工零件对应的是精品的概率,徒弟加工该零件的精品数多于师父包括三种情况,这三种情况是互斥的,根据相互独立事件同时发生的概率和互斥事件的概率得到结果.
解答:解:(1)设徒弟加工1个零件是精品的概率为p1,则
×
×
=
,∴
=
∴徒弟加工2个零件都是精品的概率是
.
(2)设徒弟加工零件的精品数多于师父的概率为p2,由(1)知p1=
,
师父加工两个零件中精品个数为0个,1个的概率分别为
,
;
徒弟加工两个零件中,精品个数为1个,2个的概率分别为
,
,
所以p2=
×
+
×
+
×
=
| 2 |
| 3 |
| 2 |
| 3 |
| p | 2 1 |
| 1 |
| 9 |
| p | 2 1 |
| 1 |
| 4 |
∴徒弟加工2个零件都是精品的概率是
| 1 |
| 4 |
(2)设徒弟加工零件的精品数多于师父的概率为p2,由(1)知p1=
| 1 |
| 2 |
师父加工两个零件中精品个数为0个,1个的概率分别为
| 1 |
| 9 |
| 4 |
| 9 |
徒弟加工两个零件中,精品个数为1个,2个的概率分别为
| 2 |
| 4 |
| 1 |
| 4 |
所以p2=
| 1 |
| 9 |
| 2 |
| 4 |
| 4 |
| 9 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 4 |
| 7 |
| 36 |
点评:本题考查相互独立事件的概率,考查互斥事件的概率,正确计算是关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
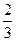 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为
 ,求
,求 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为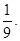 (I)求徒弟加工2个零件都是精品的概率;
(I)求徒弟加工2个零件都是精品的概率; ,求
,求