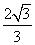题目内容
过双曲线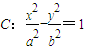 的右焦点F的直线l与双曲线右支相交于A、B两点,以线段AB为直径的圆被右准线截得的劣弧的弧度数为
的右焦点F的直线l与双曲线右支相交于A、B两点,以线段AB为直径的圆被右准线截得的劣弧的弧度数为 ,那么双曲线的离心率e=( )
,那么双曲线的离心率e=( )A.

B.
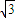
C.2
D.
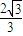
【答案】分析:由题意可得 EF=r cos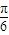 =
=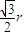 ,由直角梯形的中位线性质可得 EF=
,由直角梯形的中位线性质可得 EF=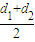 ,再由双曲线的第二定义可得
,再由双曲线的第二定义可得 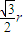 =
=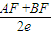 =
=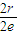 ,求得 e 的值.
,求得 e 的值.
解答:解:设A、B到右准线的距离分别等于 d1、d2,AB的中点为E,E到右准线的距离等于EF,圆的半径等于r,
则 由题意可得 EF=r cos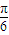 =
=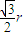 ,由直角梯形的中位线性质可得 EF=
,由直角梯形的中位线性质可得 EF=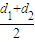 ,
,
再由双曲线的第二定义可得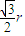 =
=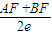 =
=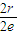 ,∴e=
,∴e=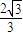 ,
,
故选 D.
点评:本题考查双曲线的定义和标准方程,以及双曲线的简单性质的应用,得到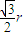 =
=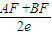 =
=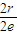 ,是解题
,是解题
的关键.
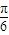 =
=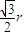 ,由直角梯形的中位线性质可得 EF=
,由直角梯形的中位线性质可得 EF=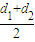 ,再由双曲线的第二定义可得
,再由双曲线的第二定义可得 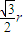 =
=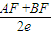 =
=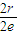 ,求得 e 的值.
,求得 e 的值.解答:解:设A、B到右准线的距离分别等于 d1、d2,AB的中点为E,E到右准线的距离等于EF,圆的半径等于r,
则 由题意可得 EF=r cos
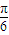 =
=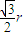 ,由直角梯形的中位线性质可得 EF=
,由直角梯形的中位线性质可得 EF=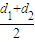 ,
,再由双曲线的第二定义可得
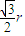 =
=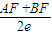 =
=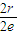 ,∴e=
,∴e=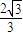 ,
,故选 D.
点评:本题考查双曲线的定义和标准方程,以及双曲线的简单性质的应用,得到
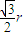 =
=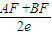 =
=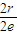 ,是解题
,是解题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
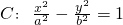 的右焦点F的直线l与双曲线右支相交于A、B两点,以线段AB为直径的圆被右准线截得的劣弧的弧度数为
的右焦点F的直线l与双曲线右支相交于A、B两点,以线段AB为直径的圆被右准线截得的劣弧的弧度数为 ,那么双曲线的离心率e=
,那么双曲线的离心率e=


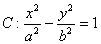 的右焦点F的直线l与双曲线右支相交于A、B两点,以线段AB为直径的圆被右准线截得的劣弧的弧度数为
的右焦点F的直线l与双曲线右支相交于A、B两点,以线段AB为直径的圆被右准线截得的劣弧的弧度数为 ,那么双曲线的离心率e= ( )
,那么双曲线的离心率e= ( )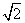 B.
B.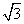 C.2 D.
C.2 D.