题目内容
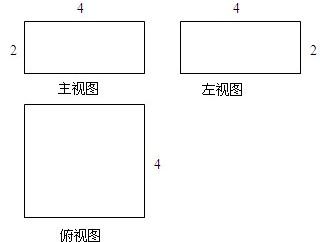
如果一个几何体的主视图与左视图都是全等的长方形,边长分别是4cm与2cm如图所示,俯视图是一个边长为4cm的正方形.(1)求该几何体的全面积.
(2)求该几何体的外接球的体积.
【答案】分析:三视图复原的几何体是底面是正方形的正四棱柱,根据三视图的数据,求出几何体的表面积,求出对角线的长,就是外接球的直径,然后求它的体积即可.
解答:解:(1)由题意可知,该几何体是长方体,
底面是正方形,边长是4,高是2,因此该
几何体的全面积是:
2×4×4+4×4×2=64cm2
几何体的全面积是64cm2.(6分)
(2)由长方体与球的性质可得,长方体的对角线是球的直径,
记长方体的对角线为d,球的半径是r,
d=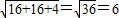 所以球的半径r=3
所以球的半径r=3
因此球的体积v=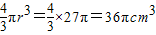 ,
,
所以外接球的体积是36πcm3.(12分)
点评:本题是基础题,考查几何体的三视图,几何体的表面积的求法,准确判断几何体的形状是解题的关键.注意正四棱柱的外接球的直径就是它的对角线的长.
解答:解:(1)由题意可知,该几何体是长方体,
底面是正方形,边长是4,高是2,因此该
几何体的全面积是:
2×4×4+4×4×2=64cm2
几何体的全面积是64cm2.(6分)
(2)由长方体与球的性质可得,长方体的对角线是球的直径,
记长方体的对角线为d,球的半径是r,
d=
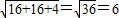 所以球的半径r=3
所以球的半径r=3因此球的体积v=
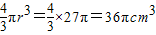 ,
,所以外接球的体积是36πcm3.(12分)
点评:本题是基础题,考查几何体的三视图,几何体的表面积的求法,准确判断几何体的形状是解题的关键.注意正四棱柱的外接球的直径就是它的对角线的长.

练习册系列答案
相关题目
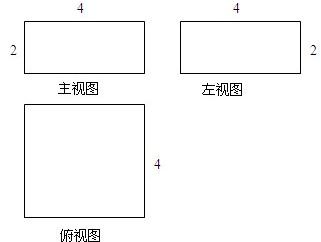
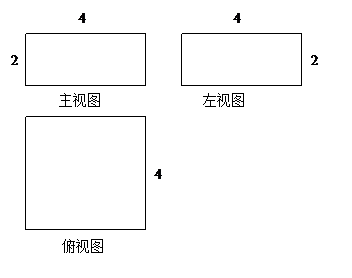 如果一个几何体的主视图与左视图都是全等的长方形,边长分别是4cm与2cm如图所示,俯视图是一个边长为4cm的正方形。
如果一个几何体的主视图与左视图都是全等的长方形,边长分别是4cm与2cm如图所示,俯视图是一个边长为4cm的正方形。