题目内容
圆c:x2+(y-1)2=1和圆c1:(x-2)2+(y-1)2=1,现构造一系列的圆c2,c3,…,cn,…,使圆cn+1同时与圆cn和圆c相切,并且都与x轴相切.①写出圆cn-1的半径rn-1与圆cn的半径rn之间关系式,并求出圆cn的半径;
②(理科做)设两个相邻圆cn和cn+1的外公切线长为ln,求
 .
.(文科做)求l1+l2+…+ln.
【答案】分析:(1)圆cn+1同时与圆cn和圆c相切,并且都与x轴相切,故可得出两个方程,化简可得圆cn-1的半径rn-1与圆cn的半径rn之间关系式,从而求出圆cn的半径;
(2)由(1)知圆心坐标,再求外公切线长,利用裂项法可求和.
解答:解:(1)由题意,c1(2,1),r1=1,设cn(xn,rn),cn-1(xn-1,rn-1),则有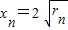 ,
,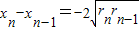 ,即
,即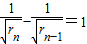 ∴
∴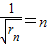 ,从而有
,从而有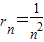 ;
;
(2)(理科)由(1)知,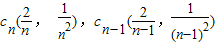 ,∴
,∴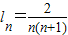 ,
,
∴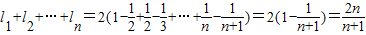 ,∴
,∴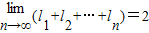 .
.
(文科)由(1)知,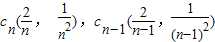 ,∴
,∴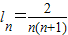 ,
,
∴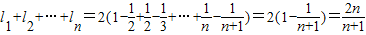 ,
,
点评:本题主要考查圆与圆相切,应充分利用两圆外切的条件,进行等价变形,对于求和利用裂项法.
(2)由(1)知圆心坐标,再求外公切线长,利用裂项法可求和.
解答:解:(1)由题意,c1(2,1),r1=1,设cn(xn,rn),cn-1(xn-1,rn-1),则有
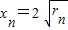 ,
,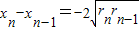 ,即
,即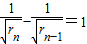 ∴
∴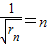 ,从而有
,从而有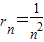 ;
;(2)(理科)由(1)知,
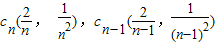 ,∴
,∴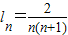 ,
,∴
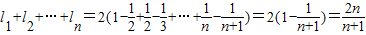 ,∴
,∴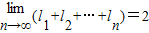 .
.(文科)由(1)知,
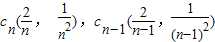 ,∴
,∴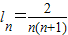 ,
,∴
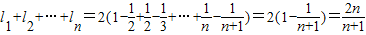 ,
,点评:本题主要考查圆与圆相切,应充分利用两圆外切的条件,进行等价变形,对于求和利用裂项法.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 (2012•浙江模拟)已知抛物线x2=4y.
(2012•浙江模拟)已知抛物线x2=4y.