题目内容
设f(x)为周期是2的奇函数,当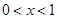 时,f(x)=x(x+1),则当
时,f(x)=x(x+1),则当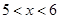 时,f(x)的表达式为
时,f(x)的表达式为
A.(x-5)(x-4) B.(x-6)(x-5) C.(x-6)(5-x) D.(x-6)(7-x)
【答案】
D
【解析】
试题分析:利用函数是奇函数,可由x∈(0,1)时的解析式求x∈(-1,0)时的解析式,利用周期性求得x∈(5,6)时,f(x)表达式.
解:因为x∈(0,1)时,f(x)=x(x+1),
设x∈(-1,0)时,-x∈(0,1),
∴f(-x)=-x(-x+1),
∵f(x)为定义在R上的奇函数
∴f(x)=-f(-x)=x(-x+1),
∴当x∈(-1,0)时,f(x)=x(-x+1),
所以x∈(5,6)时,x-6∈(-1,0),
∵f(x)为周期是2的函数,
∴f(x)=f(x-6)=(x-6)(6-x+1)=(x-6)(7-x),
故选D
考点:抽象函数的运用
点评:本题综合考查函数奇偶性与周期性知识的运用,把要求区间上的问题转化到已知区间上求解,是解题的关键,体现了转化的数学思想方法.属中档题

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 时,f(x)=x(x+1),则当
时,f(x)=x(x+1),则当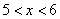 时,f(x)的表达式为
时,f(x)的表达式为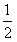 ],都有
],都有 。
。 ;
;