题目内容
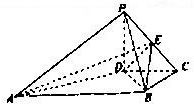
(21分).如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.

(1)证明 PA//平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C-PB-D的大小.
【答案】
解:(1)证明:连结AC,AC交BD于O.连结EO.
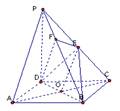
∵ 底面ABCD是正方形,∴ 点O是AC的中点.在△PAC中,EO是中位线,∴ PA//EO.而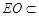 平面EDB,且
平面EDB,且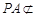 平面EDB,所以,PA//平面EDB.
平面EDB,所以,PA//平面EDB.
(2)证明:∵ PD⊥底面ABCD,且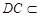 底面ABCD, ∴ PD⊥DC.
底面ABCD, ∴ PD⊥DC.
∵ 底面ABCD是正方形,有DC⊥BC, ∴ BC⊥平面PDC. 而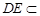 平面PDC,∴ BC⊥DE.又∵PD=DC,E是PC的中点,∴ DE⊥PC. ∴ DE⊥平面PBC.
平面PDC,∴ BC⊥DE.又∵PD=DC,E是PC的中点,∴ DE⊥PC. ∴ DE⊥平面PBC.
而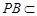 平面PBC,∴ DE⊥PB.又EF⊥PB,且
平面PBC,∴ DE⊥PB.又EF⊥PB,且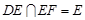 ,所以PB⊥平面EFD.
,所以PB⊥平面EFD.
(3)解:由(2))知,PB⊥DF,故∠EFD是二面角C-PB-D的平面角,由(2)知,DE⊥EF,PD⊥DB.
设正方形ABCD的边长为a,则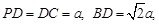
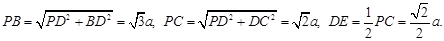
在 中,
中,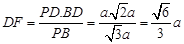 .在
.在 中,
中,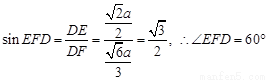 .所以,二面角C-PB-D的大小为60°.
.所以,二面角C-PB-D的大小为60°.
【解析】略

练习册系列答案
相关题目
 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,E为棱PC上异于C的一点,DE⊥BE.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,E为棱PC上异于C的一点,DE⊥BE. 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E点满足
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E点满足 (2013•南通三模)如图,在四棱锥P-ABCD中,底面ABCD是矩形,四条侧棱长均相等.
(2013•南通三模)如图,在四棱锥P-ABCD中,底面ABCD是矩形,四条侧棱长均相等.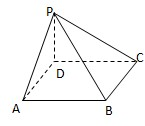 如图,在四棱锥P-ABCD中,底面ABCD是边长为的正方形,并且PD=,PA=PC=
如图,在四棱锥P-ABCD中,底面ABCD是边长为的正方形,并且PD=,PA=PC= (2012•安徽模拟)如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面四边形ABCD为直角梯形,∠B=∠C=90°,AB=3CD,∠PBC=30°,点M是PB上的动点,且
(2012•安徽模拟)如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面四边形ABCD为直角梯形,∠B=∠C=90°,AB=3CD,∠PBC=30°,点M是PB上的动点,且