题目内容
5.一种设备的价值为a元,设备维修和消耗费用第一年为b元,以后每年增加b元,用t表示设备使用的年数,且设备年平均维修、消耗费用与设备平均价值费用之和为y元,当a=450000,b=1000时,求这种设备的最佳更新年限(使用平均费用最低的t).分析 这种设备使用了t年,年平均设备维修、消耗费用为$\frac{b+2b+…+tb}{t}$=$\frac{b}{2}$ (t+1)(元).而年平均设备价值费用为$\frac{a}{t}$(元).从而y=$\frac{b}{2}$ (t+1)+$\frac{a}{t}$,利用基本不等式,即可得出结论.
解答 解:这种设备使用了t年,年平均设备维修、消耗费用为$\frac{b+2b+…+tb}{t}$=$\frac{b}{2}$ (t+1)(元).
而年平均设备价值费用为$\frac{a}{t}$(元).
从而y=$\frac{b}{2}$ (t+1)+$\frac{a}{t}$=$\frac{b}{2}$+$\frac{bt}{2}$+$\frac{a}{t}$≥$\frac{b}{2}$+$\sqrt{2ab}$,当且仅当$\frac{bt}{2}$=$\frac{a}{t}$,即t=$\sqrt{\frac{2a}{b}}$时等号成立.
当a=450 000,b=1 000时,t=$\sqrt{\frac{2×450000}{1000}}$=30(年).
因此,这种设备的最佳更新年限为30年.
点评 本题考查利用数学知识解决实际问题,考查基本不等式的运用,考查学生的计算能力,确定函数表达式是关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
15.如图所示,用符号语言可表示为( )
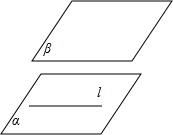

| A. | α∩β=l | B. | α∥β,l∈α | C. | l∥β,l?α | D. | α∥β,l?α |
 已知椭圆C:$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<$\sqrt{2}$),斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,向量$\overrightarrow{OA}$+$\overrightarrow{OB}$与向量$\overrightarrow{a}$=(2,-1)共线.
已知椭圆C:$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<$\sqrt{2}$),斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,向量$\overrightarrow{OA}$+$\overrightarrow{OB}$与向量$\overrightarrow{a}$=(2,-1)共线.