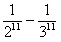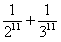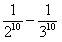题目内容
设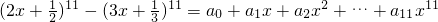 ,则|ak|(0≤k≤11)的最小值为
,则|ak|(0≤k≤11)的最小值为
- A.
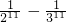
- B.
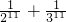
- C.
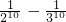
- D.
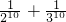
A
分析:本题主要考查了合情推理,利用归纳和类比进行简单的推理,属容易题.根据已知中T2=0,T3= -
- ,T4=0,T5=
,T4=0,T5= -
-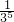 ,及,(2x+
,及,(2x+ )n-(3x+
)n-(3x+ )n=a0+a1x+a2x2+…+anxn,将|ak|(0≤k≤n)的最小值记为Tn,我们易得,当n的取值为偶数时的规律,再进一步分析,n为奇数时,Tn的值与n的关系,综合便可给出Tn的表达式.从而求出结果.
)n=a0+a1x+a2x2+…+anxn,将|ak|(0≤k≤n)的最小值记为Tn,我们易得,当n的取值为偶数时的规律,再进一步分析,n为奇数时,Tn的值与n的关系,综合便可给出Tn的表达式.从而求出结果.
解答:设n≥2,n∈N,(2x+ )n-(3x+
)n-(3x+ )n=a0+a1x+a2x2+…+anxn,将|ak|(0≤k≤n)的最小值记为Tn,根据Tn的定义,列出Tn的前几项:
)n=a0+a1x+a2x2+…+anxn,将|ak|(0≤k≤n)的最小值记为Tn,根据Tn的定义,列出Tn的前几项:
T0=0
T1= =
=
T2=0
T3= -
-
T4=0
T5= -
-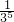
T6=0
…
由此规律,我们可以推断:Tn=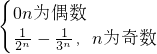
故但n=11时,|ak|(0≤k≤11)的最小值为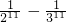 ,
,
故选A.
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).属中档题.
分析:本题主要考查了合情推理,利用归纳和类比进行简单的推理,属容易题.根据已知中T2=0,T3=
 -
- ,T4=0,T5=
,T4=0,T5= -
-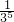 ,及,(2x+
,及,(2x+ )n-(3x+
)n-(3x+ )n=a0+a1x+a2x2+…+anxn,将|ak|(0≤k≤n)的最小值记为Tn,我们易得,当n的取值为偶数时的规律,再进一步分析,n为奇数时,Tn的值与n的关系,综合便可给出Tn的表达式.从而求出结果.
)n=a0+a1x+a2x2+…+anxn,将|ak|(0≤k≤n)的最小值记为Tn,我们易得,当n的取值为偶数时的规律,再进一步分析,n为奇数时,Tn的值与n的关系,综合便可给出Tn的表达式.从而求出结果.解答:设n≥2,n∈N,(2x+
 )n-(3x+
)n-(3x+ )n=a0+a1x+a2x2+…+anxn,将|ak|(0≤k≤n)的最小值记为Tn,根据Tn的定义,列出Tn的前几项:
)n=a0+a1x+a2x2+…+anxn,将|ak|(0≤k≤n)的最小值记为Tn,根据Tn的定义,列出Tn的前几项:T0=0
T1=
 =
=
T2=0
T3=
 -
-
T4=0
T5=
 -
-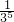
T6=0
…
由此规律,我们可以推断:Tn=
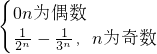
故但n=11时,|ak|(0≤k≤11)的最小值为
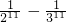 ,
,故选A.
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).属中档题.

练习册系列答案
相关题目
 (2013•松江区二模)如图所示,向量
(2013•松江区二模)如图所示,向量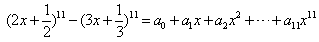 ,则|ak|(0≤k≤11)的最小值为
,则|ak|(0≤k≤11)的最小值为