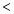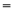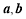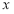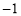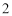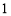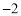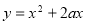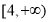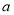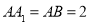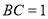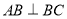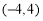题目内容
已知幂函数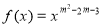 (
(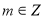 )在
)在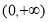 是单调减函数,且为偶函数.
是单调减函数,且为偶函数.
(1)求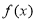 的解析式;
的解析式;
(2)讨论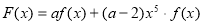 的奇偶性,并说明理由.
的奇偶性,并说明理由.
(1)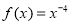 ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(Ⅰ)由幂函数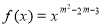 (
(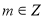 )在
)在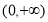 是单调减函数,且为偶函数可知
是单调减函数,且为偶函数可知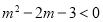 ,得
,得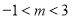 ,又因为
,又因为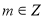 所以
所以 ;
;
(Ⅱ)由(Ⅰ)求出 ,对参数a进行讨论,再利用函数的奇偶性判断方法进行判断.
,对参数a进行讨论,再利用函数的奇偶性判断方法进行判断.
试题解析:(1)由于幂函数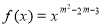 在
在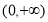 是单调减函数,
是单调减函数,
所以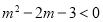 1分
1分
求得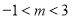 因为
因为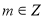 ,所以
,所以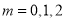 2分
2分
因为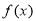 是偶函数,所以
是偶函数,所以 3分
3分
故: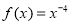 4分
4分
(2)
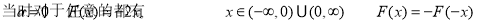
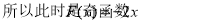 6分
6分
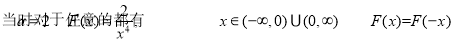
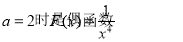 8分
8分
当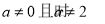 ,因为
,因为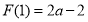 ,
,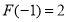 ,
,
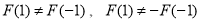 9分
9分
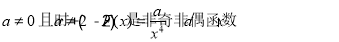 . 10分.
. 10分.
考点:1.幂函数的性质;2.函数的奇偶性.

练习册系列答案
相关题目