题目内容
已知圆的方程为x2+y2=4,过点M(2,4)作圆的两条切线,切点分别为A1、A2,直线A1A2恰好经过椭圆 的右顶点和上顶点.
的右顶点和上顶点.(Ⅰ)求椭圆的方程;
(Ⅱ)设直线x=-1与椭圆相交于A、B两点,P是椭圆上异于A、B的任意一点,直线AP、BP分别交定直线l:x=-4于两点Q、R,求证
 为定值.
为定值.
【答案】分析:(Ⅰ)利用圆的切线的性质即可求出椭圆的右顶点和上顶点,进而即可得到椭圆的方程;
(Ⅱ)设出点P的坐标,代入椭圆的方程即可得到关系式,点A,B的坐标易求出,写出直线AP,BP的方程,即可得到点Q,R的纵坐标,再利用向量的数量积即可证明.
解答:解:(Ⅰ) 观察知,x=2是圆的一条切线,切点为A1(2,0),
设O为圆心,根据圆的切线性质,MO⊥A1A2,
∴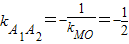 ,
,
∴直线A1A2的方程为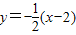 .
.
直线A1A2与y轴相交于(0,1),依题意a=2,b=1,
所求椭圆的方程为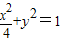 .
.
(Ⅱ)椭圆方程为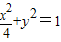 ,设P(x,y),A(-1,t),B(-1,-t),
,设P(x,y),A(-1,t),B(-1,-t),
则有 ,
,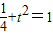 ,
,
在直线AP的方程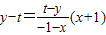 中,令x=-4,整理得
中,令x=-4,整理得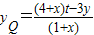 .①
.①
同理, .②
.②
①×②,并将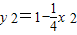 ,
,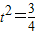 代入得yQ•yR=
代入得yQ•yR=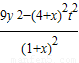
=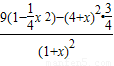 =
=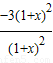 =-3.
=-3.
而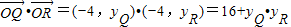 =13为定值.
=13为定值.
点评:熟练掌握圆的切线的性质、椭圆的标准方程及其性质、直线的点斜式、数量积的定义是解题的关键.注意体会设而不求的作用.
(Ⅱ)设出点P的坐标,代入椭圆的方程即可得到关系式,点A,B的坐标易求出,写出直线AP,BP的方程,即可得到点Q,R的纵坐标,再利用向量的数量积即可证明.
解答:解:(Ⅰ) 观察知,x=2是圆的一条切线,切点为A1(2,0),
设O为圆心,根据圆的切线性质,MO⊥A1A2,
∴
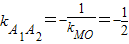 ,
,∴直线A1A2的方程为
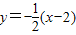 .
.直线A1A2与y轴相交于(0,1),依题意a=2,b=1,
所求椭圆的方程为
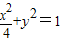 .
.(Ⅱ)椭圆方程为
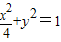 ,设P(x,y),A(-1,t),B(-1,-t),
,设P(x,y),A(-1,t),B(-1,-t),则有
 ,
,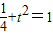 ,
,在直线AP的方程
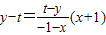 中,令x=-4,整理得
中,令x=-4,整理得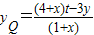 .①
.①同理,
 .②
.②①×②,并将
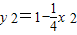 ,
,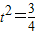 代入得yQ•yR=
代入得yQ•yR=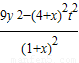
=
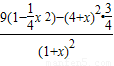 =
=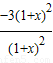 =-3.
=-3.而
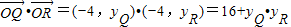 =13为定值.
=13为定值.点评:熟练掌握圆的切线的性质、椭圆的标准方程及其性质、直线的点斜式、数量积的定义是解题的关键.注意体会设而不求的作用.

练习册系列答案
相关题目
已知圆的方程为x2+y2-6x-8y=0,设该圆过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
A、10
| ||
B、20
| ||
C、30
| ||
D、40
|
 已知圆的方程为x2+y2=4,过点M(2,4)作圆的两条切线,切点分别为A1、A2,直线A1A2恰好经过椭圆
已知圆的方程为x2+y2=4,过点M(2,4)作圆的两条切线,切点分别为A1、A2,直线A1A2恰好经过椭圆