题目内容
中心在坐标原点,焦点在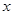 轴上的椭圆的离心率为
轴上的椭圆的离心率为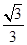 ,且经过点
,且经过点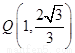 。若分别过椭圆的左右焦点
。若分别过椭圆的左右焦点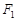 、
、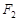 的动直线
的动直线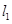 、
、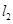 相交于P点,与椭圆分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率
相交于P点,与椭圆分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率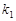 、
、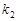 、
、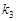 、
、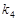 满足
满足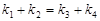 .
.
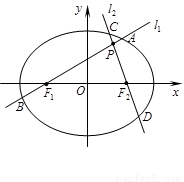
(1)求椭圆的方程;
(2)是否存在定点M、N,使得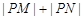 为定值.若存在,求出M、N点坐标;若不存在,说明理由.
为定值.若存在,求出M、N点坐标;若不存在,说明理由.
【答案】
(1)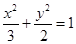 ;
;
(2)存在点M、N其坐标分别为(0 , -1)、(0, 1),使得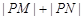 为定值
为定值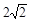 .
.
【解析】
试题分析:(1)设椭圆方程为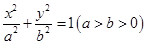 ,则由题意知
,则由题意知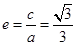 ,则
,则
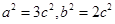 ,则椭圆方程为
,则椭圆方程为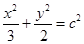 ,代入点
,代入点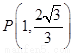 的坐标可得
的坐标可得
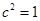 ,所求椭圆方程为
,所求椭圆方程为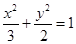
(2)当直线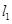 或
或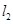 斜率不存在时,P点坐标为(-1, 0)或(1, 0).
斜率不存在时,P点坐标为(-1, 0)或(1, 0).
当直线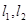 斜率存在时,设斜率分别为
斜率存在时,设斜率分别为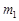 ,
,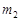 ,设
,设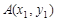 ,
,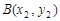 ,
,
由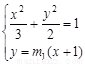 得
得 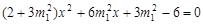 ,∴
,∴ 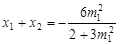 ,
,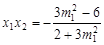 .
. 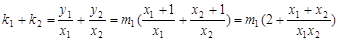
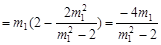 ,同理
,同理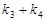
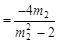 .∵
.∵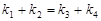 , ∴
, ∴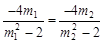 ,即
,即 .又
.又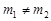 , ∴
, ∴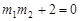 .
.
设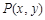 ,则
,则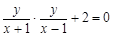 ,即
,即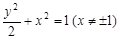 ,
,
由当直线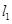 或
或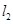 斜率不存在时,P点坐标为(-1, 0)或(1, 0)也满足,∴
斜率不存在时,P点坐标为(-1, 0)或(1, 0)也满足,∴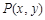 点椭圆上,则存在点M、N其坐标分别为(0 , -1)、(0, 1),使得
点椭圆上,则存在点M、N其坐标分别为(0 , -1)、(0, 1),使得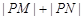 为定值
为定值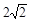 .
.
考点:本题主要考查椭圆的标准方程及几何性质,直线与椭圆的位置关系。
点评:中档题,结合椭圆的几何性质,应用“待定系数法”求得了椭圆方程。研究直线与圆锥曲线的位置关系,往往应用韦达定理,通过“整体代换”,简化解题过程,实现解题目的。(II)中对两直线斜率存在情况进行讨论,易于忽视。

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
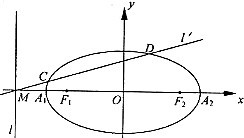 已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,
已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M, (2011•延庆县一模)已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点B与抛物线x2=4y的焦点重合,离心率
(2011•延庆县一模)已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点B与抛物线x2=4y的焦点重合,离心率