题目内容
已知两点A(-2,0),B(0,4),则线段AB的垂直平分线方程是 ( )
| A.2x+y=0 | B.2x-y+4=0 | C.x+2y-3=0 | D.x-2y+5=0 |
C
解析试题分析:出AB的中点坐标,直线AB 的斜率,然后求出AB垂线的斜率,利用点斜式方程求出线段AB的垂直平分线方程.解:两点A(-2,0),B(0,4),它的中点坐标为:(-1,2),直线AB 的斜率为: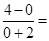 2,AB垂线的斜率为:-
2,AB垂线的斜率为:- 线段AB的垂直平分线方程是:y-2=-
线段AB的垂直平分线方程是:y-2=- (x+1),即:x+2y-3=0.故选C
(x+1),即:x+2y-3=0.故选C
考点:直线方程
点评:本题是基础题,考查中点坐标公式的应用,直线的垂线的斜率,点斜式的直线方程,考查计算能力,是送分题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
直线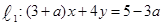 和直线
和直线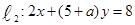 平行,则
平行,则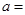 ( )
( )
A.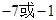 | B.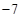 | C.7或1 | D.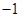 |
抛物线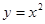 上的任意一点到直线
上的任意一点到直线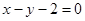 的最短距离为( )
的最短距离为( )
A.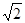 | B. | C.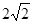 | D.以上答案都不对 |
直线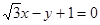 的倾斜角是( )
的倾斜角是( )
| A.30° | B.60° | C.120° | D.150° |
已知直线l: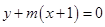 与直线
与直线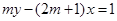 平行,则直线l在
平行,则直线l在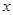 轴上的截距是( )
轴上的截距是( )
| A.1 | B.-1 | C.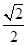 | D.-2 |
若直线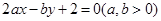 始终平分圆
始终平分圆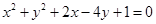 的周长,则
的周长,则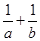 的最小值为( ).
的最小值为( ).
A.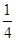 | B. | C. | D.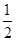 |
直线x+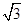 y-1=0的倾斜角是( )
y-1=0的倾斜角是( )
| A.150º | B.135º | C.120º | D.30º |
三角形的三个顶点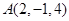 、
、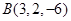 、
、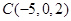 ,则
,则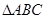 的中线
的中线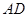 的长为( ).
的长为( ).
| A.49 | B.9 | C.7 | D.3 |
已知点A(-1,0);B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是
| A.(0,1) | B.(1-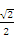 , , ) ( ) ( | C.(1-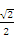 , ,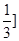 | D.[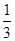 , , ) ) |