题目内容
【题目】在等差数列{an}中,a14+a15+a16=﹣54,a9=﹣36,Sn为其前n项和.
(1)求Sn的最小值,并求出相应的n值;
(2)求Tn=|a1|+|a2|+…+|an|.
【答案】
(1)解:设等差数列{an}的公差为d,
∵a14+a15+a16=3a15=﹣54,a15=﹣18,
∴ ![]() ,
,
∴an=a9+(n﹣9)×d=3n﹣63,
∴an+1=3(n+1)﹣63=3n﹣60
令 ![]() ,
,
∴20≤n≤21,
∴ ![]() ,
,
即当n=20或21时,Sn最小且最小值为﹣630
(2)解:∵a1=﹣60,d=3,
∴an=﹣60+(n﹣1)×3=3n﹣63,
由an=3n﹣63≥0,得n≥21,
∵a20=3×20﹣63=﹣3<0,a21=3×21﹣63=0,
∴数列{an}中,前20项小于0,第21项等于0,以后各项均为正数,
当n≤21时, ![]()
当n≥22时, 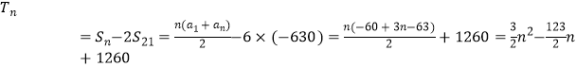
综上, 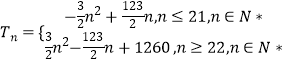
【解析】(1)由已知条件求出d=3,令 ![]() ,求出n的范围,求出Sn的最小值.(2)数列{an}中,前20项小于0,第21项等于0,以后各项均为正数,所以当n≤21时,Tn=﹣Sn , 当n>21时,Tn=Sn﹣2S21 , 由此利用分类讨论思想能求出Tn .
,求出n的范围,求出Sn的最小值.(2)数列{an}中,前20项小于0,第21项等于0,以后各项均为正数,所以当n≤21时,Tn=﹣Sn , 当n>21时,Tn=Sn﹣2S21 , 由此利用分类讨论思想能求出Tn .

 阅读快车系列答案
阅读快车系列答案【题目】某港口的水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下面是每天时间与水深的关系表:
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 10 | 13 | 9.9 | 7 | 10 | 13 | 10.1 | 7 | 10 |
经过长期观测,y=f(t)可近似的看成是函数y=Asinωt+b
(1)根据以上数据,求出y=f(t)的解析式;
(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
【题目】某人射击一次命中7~10环的概率如下表
命中环数 | 7 | 8 | 9 | 10 |
命中概率 | 0.16 | 0.19 | 0.28 | 0.24 |
计算这名射手在一次射击中:
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数不足8环的概率.

