题目内容
已知点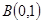 ,点
,点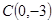 ,直线
,直线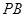 、
、 都是圆
都是圆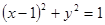 的切线(
的切线(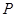 点不在
点不在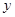 轴上)。
轴上)。
⑴求过点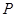 且焦点在
且焦点在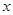 轴上抛物线的标准方程;
轴上抛物线的标准方程;
⑵过点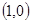 作直线
作直线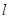 与⑴中的抛物线相交于
与⑴中的抛物线相交于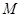 、
、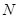 两点,问是否存在定点
两点,问是否存在定点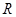 ,使
,使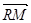 .
.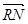 为常数?若存在,求出点
为常数?若存在,求出点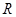 的坐标与常数;若不存在,请说明理由。
的坐标与常数;若不存在,请说明理由。
【答案】
(1) 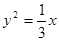 (2) 定点
(2) 定点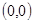
【解析】
试题分析:①设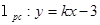 得到
得到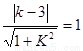 解得
解得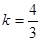 (2分)
(2分)
得到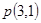 代入
代入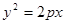 中 ,解得
中 ,解得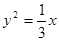 (4分)
(4分)
②联立 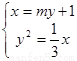 得到
得到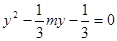 ,
,
有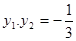 ,
,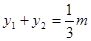 (6分)
(6分)
设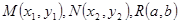
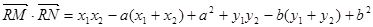

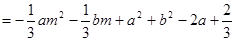 (9分)
(9分)
当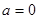 且
且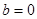 时,
时,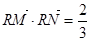 ,即定点
,即定点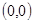 (12分)
(12分)
考点:抛物线方程,直线与抛物线位置关系
点评:解决该试题的关键是熟悉点到直线距离公式,以及抛物线方程与点的关系,求解得到方程,同时结合向量的数量积来确定结论,属于中档题。

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
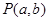 与点
与点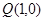 在直线
在直线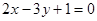 的两侧,则下列说法:
的两侧,则下列说法: ;
; 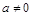 时,
时,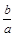 有最小值,无最大值;
有最小值,无最大值;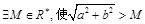 恒成立
恒成立 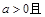
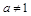 ,
,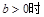 , 则
, 则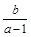 的取值范围为(-
的取值范围为(-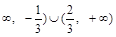
 的方程
的方程 在
在 没有实数根,则
没有实数根,则 的取值范围是
的取值范围是
 与直线
与直线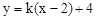 有两个交点时,实数
有两个交点时,实数 的取值范围
的取值范围
 与点
与点 在直线
在直线 两侧, 则
两侧, 则 .
. 的图像向右平移
的图像向右平移 个单位后变为偶函数,则
个单位后变为偶函数,则

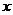 的方程
的方程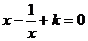 在
在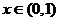 没有实数根,则
没有实数根,则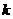 的取值范围是
的取值范围是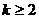 .
.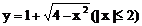 与直线
与直线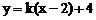 有两个交点时,实数
有两个交点时,实数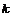 的取值范围是
的取值范围是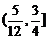 .
.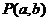 与点
与点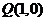 在直线
在直线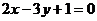 两侧, 则
两侧, 则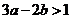 .
. 的图像向右平移
的图像向右平移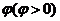 个单位后变为偶函数,则
个单位后变为偶函数,则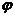 的最小值是
的最小值是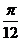 .
.