题目内容
 如图,已知两个正方行ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
如图,已知两个正方行ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.(1)若平面ABCD⊥平面DCEF,求直线MN与平面DCEF所成角的正值弦;
(2)用反证法证明:直线ME与BN是两条异面直线.
分析:(1)(解法一)由面面垂直的性质定理,取CD的中点G,连接MG,NG,再证出∠MNG是所求的角,在△MNG中求解;
(解法二)由垂直关系建立空间直角坐标系,求出平面DCEF的法向量,再用向量的数量积求解;
(2)由题意假设共面,由AB∥CD推出AB∥平面DCEF,再推出AB∥EN,由得到EN∥EF,即推出矛盾,故假设不成立;
(解法二)由垂直关系建立空间直角坐标系,求出平面DCEF的法向量,再用向量的数量积求解;
(2)由题意假设共面,由AB∥CD推出AB∥平面DCEF,再推出AB∥EN,由得到EN∥EF,即推出矛盾,故假设不成立;
解答:解:(1)解法一:
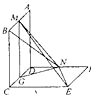
取CD的中点G,连接MG,NG.设正方形ABCD,DCEF的边长为2,
则MG⊥CD,MG=2,NG=
.
∵平面ABCD⊥平面DCED,
∴MG⊥平面DCEF,
∴∠MNG是MN与平面DCEF所成的角.
∵MN=
=
,∴sin∠MNG=
为MN与平面DCEF所成角的正弦值
解法二:
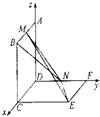
设正方形ABCD,DCEF的边长为2,以D为坐标原点,
分别以射线DC,DF,DA为x,y,z轴正半轴建立空间直角坐标系如图.
则M(1,0,2),N(0,1,0),可得
=(-1,1,-2).
又∵
=(0,0,2)为平面DCEF的法向量,
∴cos(
,
)=
=-
•
∴MN与平面DCEF所成角的正弦值为cos(
,
)=
•
(2)假设直线ME与BN共面,
则AB?平面MBEN,且平面MBEN与平面DCEF交于EN
由已知,两正方形不共面,∴AB?平面DCEF.
又∵AB∥CD,∴AB∥平面DCEF.
∵面EN为平面MBEN与平面DCEF的交线,∴AB∥EN.
又∵AB∥CD∥EF,
∴EN∥EF,这与EN∩EF=E矛盾,故假设不成立.
∴ME与BN不共面,它们是异面直线.

取CD的中点G,连接MG,NG.设正方形ABCD,DCEF的边长为2,
则MG⊥CD,MG=2,NG=
| 2 |
∵平面ABCD⊥平面DCED,
∴MG⊥平面DCEF,
∴∠MNG是MN与平面DCEF所成的角.
∵MN=
| MG2+GN2 |
| 6 |
| ||
| 3 |
解法二:

设正方形ABCD,DCEF的边长为2,以D为坐标原点,
分别以射线DC,DF,DA为x,y,z轴正半轴建立空间直角坐标系如图.
则M(1,0,2),N(0,1,0),可得
| MN |
又∵
| DA |
∴cos(
| MN |
| DA |
| ||||
||
|
| ||
| 3 |
∴MN与平面DCEF所成角的正弦值为cos(
| MN |
| DA |
| ||
| 3 |
(2)假设直线ME与BN共面,
则AB?平面MBEN,且平面MBEN与平面DCEF交于EN
由已知,两正方形不共面,∴AB?平面DCEF.
又∵AB∥CD,∴AB∥平面DCEF.
∵面EN为平面MBEN与平面DCEF的交线,∴AB∥EN.
又∵AB∥CD∥EF,
∴EN∥EF,这与EN∩EF=E矛盾,故假设不成立.
∴ME与BN不共面,它们是异面直线.
点评:本题考查了线面角的求法,可有面面垂直的性质定理用两种方法来求解;还考查了用反证法证明,用了线线平行与线面平行的相互转化来推出矛盾,考查了推理论证能力和逻辑思维能力.

练习册系列答案
相关题目


 如图,已知两个正方行ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
如图,已知两个正方行ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点. 如图,已知两个正方行ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
如图,已知两个正方行ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.