题目内容
(本题满分10分) 如图,在平行四边形 中,
中, ,将
,将 沿
沿 折起到
折起到 的位置,使平面
的位置,使平面 平面
平面 .
.
(1)求二面角E-AB-D的大小;
(2)求四面体 的表面积和体积.
的表面积和体积.

【答案】
(1)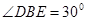 (或证
(或证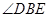 即为
即为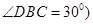 .(2)
.(2)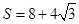 ,V=
,V=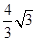
【解析】
试题分析:(1)在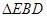 中,
中,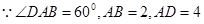 ,
,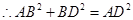 ,
,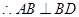 因为平面
因为平面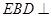 平面
平面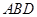 ,所以
,所以
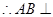 平面
平面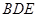 ,
,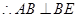 .
.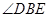 即为二面角
即为二面角 的平面角.
的平面角.
解三角形得到。
(2)在第一问的基础上,进一步得到体高,和边长,求解表面积和体积。
(1)在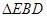 中,
中,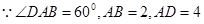 ,
,
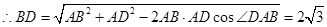 .
.
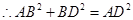 ,
,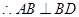
因为平面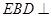 平面
平面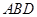 ,所以
,所以
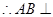 平面
平面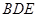 ,
,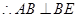 .
.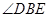 即为二面角
即为二面角 的平面角.
的平面角.
又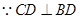 ,
, ,而
,而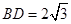 ,
,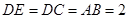 ,
,
故在直角三角形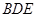 中,
中,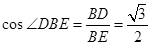 ,
,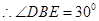 (或证
(或证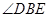 即为
即为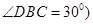 .
.
(2)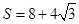 ,V=
,V=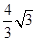
考点:本题主要是考查二面角的平面角的求解,以及四面体的表面积和体积的运算问题。
点评:解决该试题的关键是利用三垂线定理作出二面角的平面角,以及利用特殊三角形的面积得到表面积和四面体体积。

练习册系列答案
相关题目
 ,求证:
,求证: ;
; ,求证:三数
,求证:三数 ,
, ,
, 中至少有一个不小于2.
中至少有一个不小于2.
 的所有棱长都为2,
的所有棱长都为2, 为棱
为棱 的中点,
的中点, 平面
平面 ;
; 的余弦值大小.
的余弦值大小.
 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和 两点,现测得
两点,现测得 ,
, ,
, ,
, ,
, ,求两景点
,求两景点