题目内容
已知直线3x+4y-12=0与x轴、y轴相交于A,B两点,点C在圆(x-5)2+(y-6)2=9上移动,则△ABC面积的最大值和最小值之差为
15
15
.分析:作出与已知直线平行且与圆(x-5)2+(y-6)2=9相切的直线,切点分别为P1、P2,如图所示.由圆的性质和三角形面积公式可得动点C分别与P1、P2重合时,△ABC面积达到最小值和最大值.因此△ABC面积的最大值、最小值之差为S△ABP2-S△ABP1=
(d2-d1),结合圆的切线的性质得到d2-d1等于直径,由此即可算出△ABC面积的最大值和最小值之差.
| 5 |
| 2 |
解答:解:设作出与已知直线平行且与圆(x-5)2+(y-6)2=9相切的直线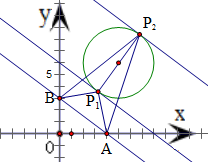 ,
,
切点分别为P1、P2,如图所示
则动点C在圆(x-5)2+(y-6)2=9上移动时,若C与点P1重合时,
△ABC面积达到最小值;而C与点P2重合时,△ABC面积达到最大值
∵直线3x+4y-12=0与x轴、y轴相交于A(4,0)、B(0,3)两点
可得|AB|=
=5
∴△ABC面积的最大值和最小值之差为
S=S△ABP2-S△ABP1=
|AB|(d2-d1)=
(d2-d1),
其中d2、d1分别为点P2、点P1到直线AB的距离
∵P1、P2是圆(x-5)2+(y-6)2=9的两条平行切线
∴点P2、点P1到直线AB的距离之差等于圆的直径,即d2-d1=6
因此△ABC面积的最大值和最小值之差为
(d2-d1)=
×6=15
故答案为:15
 ,
,切点分别为P1、P2,如图所示
则动点C在圆(x-5)2+(y-6)2=9上移动时,若C与点P1重合时,
△ABC面积达到最小值;而C与点P2重合时,△ABC面积达到最大值
∵直线3x+4y-12=0与x轴、y轴相交于A(4,0)、B(0,3)两点
可得|AB|=
| 42+32 |
∴△ABC面积的最大值和最小值之差为
S=S△ABP2-S△ABP1=
| 1 |
| 2 |
| 5 |
| 2 |
其中d2、d1分别为点P2、点P1到直线AB的距离
∵P1、P2是圆(x-5)2+(y-6)2=9的两条平行切线
∴点P2、点P1到直线AB的距离之差等于圆的直径,即d2-d1=6
因此△ABC面积的最大值和最小值之差为
| 5 |
| 2 |
| 5 |
| 2 |
故答案为:15
点评:本题给出线段AB和圆上的动点C,求三角形ABC面积的最大值与最小值之差.着重考查了圆的性质、直线与圆的位置关系和三角形的面积计算等知识,属于中档题.

练习册系列答案
相关题目