题目内容
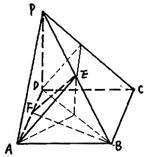
一个多面体的直观图及三视图如图所示(其中E、F分别是PB、AD的中点).
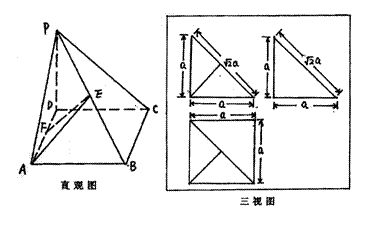
(Ⅰ)求证:EF⊥平面PBC;
(Ⅱ)求三棱锥B—AEF的体积。

(Ⅰ)求证:EF⊥平面PBC;
(Ⅱ)求三棱锥B—AEF的体积。
(1)见解析(2)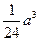
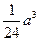
(Ⅰ)取PC的中点G,连结EG,GD,则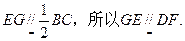
由(Ⅰ)知FD⊥平面PDC,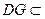 面PDC,所以FD⊥DG。
面PDC,所以FD⊥DG。
所以四边形FEGD为矩形,因为G为等腰Rt△RPD斜边PC的中点,
所以DG⊥PC,
又DG⊥GE,PC∩EG=E,所以DG⊥平面PBC.
因为DG//EF,所以EF⊥平面PBC。
(Ⅱ)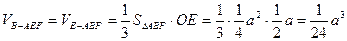
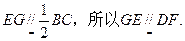
由(Ⅰ)知FD⊥平面PDC,
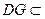 面PDC,所以FD⊥DG。
面PDC,所以FD⊥DG。所以四边形FEGD为矩形,因为G为等腰Rt△RPD斜边PC的中点,
所以DG⊥PC,
|
因为DG//EF,所以EF⊥平面PBC。
(Ⅱ)
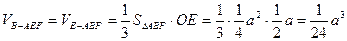

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,底面
中,底面 为矩形,
为矩形, 底面
底面 ,
,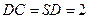 ,点
,点 在侧棱
在侧棱 上,
上,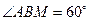 。
。
 的大小。
的大小。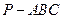 中,⊿
中,⊿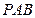 是等边三角形,∠PAC=∠PBC="90" º.
是等边三角形,∠PAC=∠PBC="90" º.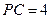 ,且平面
,且平面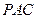 ⊥平面
⊥平面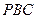 ,求三棱锥
,求三棱锥
 ,则直线l的垂线必平行平面
,则直线l的垂线必平行平面
 的三视图如图所 示,其中
的三视图如图所 示,其中 分别是
分别是 五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形
五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形 为正方形且
为正方形且 ;在左视图中
;在左视图中 俯视图中
俯视图中 ,
, 作平面
作平面 的垂线,若垂足H在直线
的垂线,若垂足H在直线 上,求证:平面
上,求证:平面 ⊥平面
⊥平面 ;
; 的体积及其外接球的表面积.
的体积及其外接球的表面积. 中,
中,  底面
底面 ,
,
 .
.
 分别为棱
分别为棱 的中点,求证:
的中点,求证: 平面
平面 ;
;
 (2)在四棱锥G—ABCD中,过点B作平面
(2)在四棱锥G—ABCD中,过点B作平面