题目内容
已知f(x)=log
 (a>0且a≠1).
(a>0且a≠1).
(1)求f(x)的 定义域;
(2)判断f(x)的奇偶性并予以证明.
【答案】
(1)定义域是(-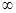 ,-1)
,-1) ; (2) 见解析。
; (2) 见解析。
【解析】本试题主要是考查了函数的定义域和函数奇偶性的判定问题。
(1)因为给出对数式,则真数大于零,由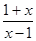 >0得定义域是(-
>0得定义域是(-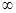 ,-1)
,-1) ;
;
(2)然后在第一问的基础上,判定f(-x)+ f(x)=0的情况可以得到结论。
解:(1) 由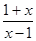 >0得,定义域是(-
>0得,定义域是(-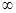 ,-1)
,-1) ;
;
(2) 定义域(-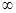 ,-1)
,-1) 是关于原点对称,
是关于原点对称,
又由f(-x)+ f(x)=0得f(-x)=- f(x), 所以f(x)是奇函数。

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目