题目内容
9.Sn为数列{2n+1}的前n项和,求数列{$\frac{1}{{S}_{n}}$}的前n项和为$\frac{3}{4}-\frac{1}{2(n+1)}-\frac{1}{2(n+2)}$.分析 由等差数列的求和公式求得数列{2n+1}的前n项和,代入数列{$\frac{1}{{S}_{n}}$}后由裂项相消法求得数列{$\frac{1}{{S}_{n}}$}的前n项和.
解答 解:由题意,Sn=3+5+7+…+(2n+1)=$\frac{(3+2n+1)n}{2}=n(n+2)$,
∴$\frac{1}{{S}_{n}}=\frac{1}{n(n+2)}=\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,
设数列{$\frac{1}{{S}_{n}}$}的前n项和为Tn,
则${T}_{n}=\frac{1}{2}(1-\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{n-1}-\frac{1}{n+1}+\frac{1}{n}-\frac{1}{n+2})$
=$\frac{1}{2}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})=\frac{1}{2}(\frac{3}{2}-\frac{1}{n+1}-\frac{1}{n+2})$
=$\frac{3}{4}-\frac{1}{2(n+1)}-\frac{1}{2(n+2)}$.
点评 本题考查了等差数列的前n项和,考查了裂项相消法求数列的和,是中档题.

练习册系列答案
相关题目
14.直线x+ay+1=0与圆x2+(y-1)2=4的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
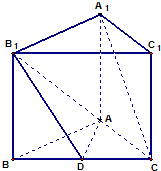 在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10,A1A=6,D是BC边的中点.
在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10,A1A=6,D是BC边的中点.