题目内容
将八个半径都为1的球分放两层放置在一个圆柱内，并使得每个球都和其相邻的四个球相切，且与圆柱的一个底面及侧面都相切，则此圆柱的高等于
2+
| 4 | 8 |
2+
．| 4 | 8 |
分析：将球的球心作为几何体的顶点，构造一新几何体，求出该几何的高，则此圆柱的高等于新几何体的高加两个半径，从而得到结论．
解答：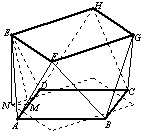
解：如图，ABCD是下层四个球的球心，EFGH是上层的四个球心．每个球心与其相切的球的球心距离=2．EFGH在平面ABCD上的射影是一个正方形．是把正方形ABCD绕其中心旋转45°而得．设E的射影为N，则MN=
-1，EM=
，故EN2=3-（
-1）2=2
∴EN=
所以圆柱的高为2+
故答案为：2+
解：如图，ABCD是下层四个球的球心，EFGH是上层的四个球心．每个球心与其相切的球的球心距离=2．EFGH在平面ABCD上的射影是一个正方形．是把正方形ABCD绕其中心旋转45°而得．设E的射影为N，则MN=| 2 |
| 3 |
| 2 |
| 2 |
∴EN=
| 4 | 8 |
所以圆柱的高为2+
| 4 | 8 |
故答案为：2+
| 4 | 8 |
点评：本题主要考查了空间位置关系与距离，同时考查了空间想象能力和计算能力，属于中档题．
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目