题目内容
设双曲线C: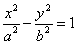 (a>0,b>0)的离心率为e,若直线l: x=
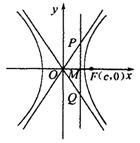
(a>0,b>0)的离心率为e,若直线l: x=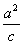 与两条渐近线相交于P、Q两点,F为右焦点,△FPQ为等边三角形.
与两条渐近线相交于P、Q两点,F为右焦点,△FPQ为等边三角形.
(1)求双曲线C的离心率e的值;
(2)若双曲线C被直线y=ax+b截得的弦长为 ,求双曲线c的方程.
,求双曲线c的方程.
【答案】
解析:(1)双曲线C的右准线l的方程为:x=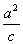 ,两条渐近线方程为:
,两条渐近线方程为: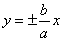 .
.
 ∴ 两交点坐标为
∴ 两交点坐标为 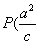 ,
, 、
、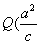 ,
,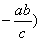 .
.
∵ △PFQ为等边三角形,则有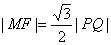 (如图).
(如图).
∴ 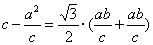 ,即
,即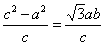 .
.
解得 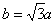 ,c=2a.∴
,c=2a.∴ 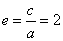 .……………………………………6分
.……………………………………6分
(2)由(1)得双曲线C的方程为把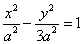 .
.
把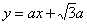 代入得
代入得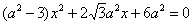 .
.
依题意  ∴
∴ 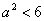 ,且
,且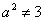 .
.
∴ 双曲线C被直线y=ax+b截得的弦长为

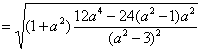
∵ 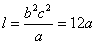 . ∴
. ∴  .
.
整理得 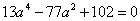 .
.
∴ 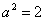 或
或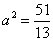 .
.
∴ 双曲线C的方程为: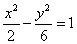 或
或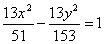 .……………… 12分
.……………… 12分

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 (a>0,b>0)的右焦点为F,O为坐标原点.若以F为圆心,FO为半径的圆与双曲线C的一条渐近线交于点A(不同于O点),则△OAF的面积为
(a>0,b>0)的右焦点为F,O为坐标原点.若以F为圆心,FO为半径的圆与双曲线C的一条渐近线交于点A(不同于O点),则△OAF的面积为
 (a>0,b>0)的右焦点为F,O为坐标原点.若以F为圆心,FO为半径的圆与双曲线C的一条渐近线交于点A(不同于O点),则△OAF的面积为
(a>0,b>0)的右焦点为F,O为坐标原点.若以F为圆心,FO为半径的圆与双曲线C的一条渐近线交于点A(不同于O点),则△OAF的面积为
 (a>0,b>0)的离心率为e,若直线l: x=
(a>0,b>0)的离心率为e,若直线l: x= 与两条渐近线相交于P、Q两点,F为右焦点,△FPQ为等边三角形.
与两条渐近线相交于P、Q两点,F为右焦点,△FPQ为等边三角形. ,求双曲线c的方程.
,求双曲线c的方程.