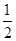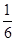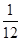题目内容
为了提高食品的安全度,某食品安检部门调查了一个海水养殖场的养殖鱼的有关情况,安检人员从这个海水养殖场中不同位置共捕捞出100条鱼,称得每条鱼的质量(单位:kg),并将所得数据进行统计得下表.若规定超过正常生长速度(1.0~1.2 kg/年)的比例超过15%,则认为所饲养的鱼有问题,否则认为所饲养的鱼没有问题.
(1)根据数据统计表,估计数据落在[1.20,1.30)中的概率约为多少,并判断此养殖场所饲养的鱼是否存在问题?
(2)上面捕捞的100条鱼中间,从质量在[1.00,1.05)和[1.25,1.30)的鱼中,任取2条鱼来检测,求恰好所取得的鱼的质量在[1.00,1.05)和[1.25,1.30)各有1条的概率.
| 鱼的 质量 | [1.00, 1.05) | [1.05, 1.10) | [1.10, 1.15) | [1.15, 1.20) | [1.20, 1.25) | [1.25, 1.30) |
| 鱼的 条数 | 3 | 20 | 35 | 31 | 9 | 2 |
(2)上面捕捞的100条鱼中间,从质量在[1.00,1.05)和[1.25,1.30)的鱼中,任取2条鱼来检测,求恰好所取得的鱼的质量在[1.00,1.05)和[1.25,1.30)各有1条的概率.
(1) 没有问题 (2)

(1)捕捞的100条鱼中间,数据落在[1.20,1.25)的概率约为P1=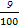 =0.09;
=0.09;
数据落在[1.25,1.30)的概率约为P2=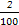 =0.02;
=0.02;
所以数据落在[1.20,1.30)中的概率约为P=P1+P2=0.11.
由于0.11×100%=11%<15%,
故饲养的这批鱼没有问题.
(2)质量在[1.00,1.05)的鱼有3条,把这3条鱼分别记作A1,A2,A3,
质量在[1.25,1.30)的鱼有2条,分别记作B1,B2,那么所有的可能结果有:
{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},
{A2,B1}{A2,B2},{A3,B1},{A3,B2},{B1,B2},共10种,
而恰好所取得的鱼的质量在[1.00,1.05)和[1.25,1.30)各有1条有:{A1,B1},
{A1,B2},{A2,B1},{A2,B2},{A3,B1},{A3,B2},共6种,所以恰好所取得的鱼的质量在[1.00,1.05)和[1.25,1.30)各有1条的概率为 =
= .
.
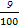 =0.09;
=0.09;数据落在[1.25,1.30)的概率约为P2=
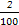 =0.02;
=0.02;所以数据落在[1.20,1.30)中的概率约为P=P1+P2=0.11.
由于0.11×100%=11%<15%,
故饲养的这批鱼没有问题.
(2)质量在[1.00,1.05)的鱼有3条,把这3条鱼分别记作A1,A2,A3,
质量在[1.25,1.30)的鱼有2条,分别记作B1,B2,那么所有的可能结果有:
{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},
{A2,B1}{A2,B2},{A3,B1},{A3,B2},{B1,B2},共10种,
而恰好所取得的鱼的质量在[1.00,1.05)和[1.25,1.30)各有1条有:{A1,B1},
{A1,B2},{A2,B1},{A2,B2},{A3,B1},{A3,B2},共6种,所以恰好所取得的鱼的质量在[1.00,1.05)和[1.25,1.30)各有1条的概率为
 =
= .
.
练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目