题目内容
定义:如果数列![]() 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称![]() 为“三角形”数列.对于“三角形”数列
为“三角形”数列.对于“三角形”数列![]() ,如果函数
,如果函数![]() 使得
使得![]() 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称![]() 是数列
是数列![]() 的“保三角形函数”,
的“保三角形函数”,![]() .
.
(1)已知![]() 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若![]() 是数列
是数列![]() 的“保三角形函数”,求k的取值范围;
的“保三角形函数”,求k的取值范围;
(2)已知数列![]() 的首项为2010,
的首项为2010,![]() 是数列
是数列![]() 的前n项和,且满足
的前n项和,且满足![]() ,证明
,证明![]() 是“三角形”数列;
是“三角形”数列;
(3) 若![]() 是(2)中数列
是(2)中数列![]() 的“保三角形函数”,问数列
的“保三角形函数”,问数列![]() 最多有多少项.
最多有多少项.
解:(1)显然![]() ,
,![]() 对任意正整数都成立,即
对任意正整数都成立,即![]() 是三角形数列.
是三角形数列.
因为k>1,显然有![]() ,由
,由![]() 得
得![]() ,解得
,解得![]() .
.
所以当![]() 时,
时,![]() 是数列
是数列![]() 的“保三角形函数”.
的“保三角形函数”.
(2) 由![]() 得
得![]() ,两式相减得
,两式相减得![]()
所以,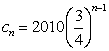 ,经检验,此通项公式满足
,经检验,此通项公式满足![]()
显然![]() ,因为
,因为![]() ,
,
所以![]() 是“三角形”数列.
是“三角形”数列.
(3) 因为![]() 是单调递减函数,所以,由
是单调递减函数,所以,由![]() 得
得
![]()
化简得![]() ,解得
,解得![]() ,即数列
,即数列![]() 最多有26项.
最多有26项.

练习册系列答案
相关题目
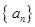 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称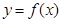 使得
使得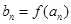 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称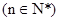 .
.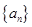 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若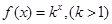 是数列
是数列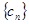 的首项为2010,
的首项为2010,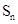 是数列
是数列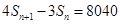 ,证明
,证明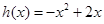 ,
,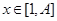 ,和数列1,
,和数列1,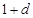 ,
,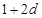 ,(
,(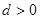 )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由. 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称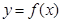 使得
使得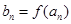 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称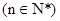 .
.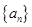 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若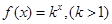 是数列
是数列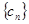 的首项为2010,
的首项为2010,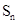 是数列
是数列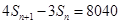 ,证明
,证明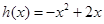 ,
,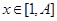 ,和数列1,
,和数列1,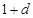 ,
,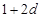 ,(
,(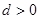 )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由.