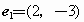题目内容
设
，
为基底向量，已知向量
=
-k
，
=2
+
，
=3
-
，若A，B，D三点共线，则实数k的值等于（ ）
. |
| a |
. |
| b |
. |
| AB |
. |
| a |
. |
| b |
. |
| CB |
. |
| a |
. |
| b |
. |
| CD |
. |
| a |
. |
| b |
| A、-2 | B、2 | C、-10 | D、10 |
分析：由题意先求出
，再由A，B，D三点共线得
=λ
，根据方程两边对应向量的系数相等求出k的值．
| BD |
. |
| AB |
| BD |
解答：解：由题意得，
=
-
=（3
-
）-（2
+
）=
-2
，
∵A，B，D三点共线，∴
=λ
，则
-k
=λ（
-2
），
解得λ=1，k=2．
故选B．
| BD |
. |
| CD |
| CB |
. |
| a |
. |
| b |
. |
| a |
. |
| b |
. |
| a |
. |
| b |
∵A，B，D三点共线，∴
. |
| AB |
| BD |
. |
| a |
. |
| b |
. |
| a |
. |
| b |
解得λ=1，k=2．
故选B．
点评：本题考查了向量共线定理的应用，即由题意构造向量并表示出向量，利用方程思想求出参数的值．
练习册系列答案
相关题目
选择题：
(1)
如果a，b是两个单位向量，那么下列四个结论中正确的是[
]|
(A)a ＝b |
(B)a ·b＝1 |
|
(C) |
(D) |
(2)
对于任意向量a、b，下列命题中正确的是[
](A)
若a，b满足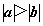
，且a与b同向，则a＞b
(B)
(C)
(D)
(3)在四边形ABCD中，若
，则
[
]|
(A)ABCD 是矩形 |
(B)ABCD 是菱形 |
|
(C)ABCD 是正方形 |
(D)ABCD 是平行四边形 |
(4)
设a是非零向量，λ是非零实数，下列结论中正确的是[
]|
(A)a 与－λa的方向相反 |
(B) |
|
(C)a 与 的方向相同 |
(D) |
(5)
设M是□ABCD的对角线的交点，O为任意一点，则
等于
[
]|
(A) |
(B)2 |
(C)3 |
(D)4 |
(6)
下列各组向量中，可以作为基底的是[
](A)
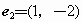
(B)
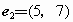
(C)
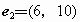
(D)
