题目内容
(本题14分)如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点.
 (1)FD∥平面ABC;
(1)FD∥平面ABC;
(2)AF⊥平面EDB.
解析:如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点.
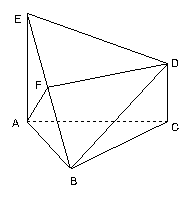
![]() (1)FD∥平面ABC;(2)AF⊥平面EDB.
(1)FD∥平面ABC;(2)AF⊥平面EDB.
证明:(1)取AB的中点M,连FM,MC,
∵ F、M分别是BE、BA的中点,
∴ FM∥EA,FM=![]() EA.
EA.
∵ EA、CD都垂直于平面ABC,
∴ CD∥EA,∴ CD∥FM. ………………3分
又 DC=a,∴FM=DC.
∴四边形FMCD是平行四边形,
∴ FD∥MC.即FD∥平面ABC. ……………7分
(2)∵M是AB的中点,△ABC是正三角形,
∴CM⊥AB,又CM⊥AE,
∴CM⊥面EAB,CM⊥AF,FD⊥AF, ………………………………11分
又F是BE的中点,EA=AB,∴AF⊥EB.
即由AF⊥FD,AF⊥EB,FD∩EB=F,
可得AF⊥平面EDB. ……………………………………………………14分

练习册系列答案
相关题目

 如图,
如图,

 中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点
中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点