题目内容
（本题14分）
如图，四棱锥
中,底面ABCD是矩形，PA⊥平面ABCD，PA=AB=1，BC=2，E为PD的中点
（1）求异面直线PA与CE所成角的大小；
（2）（理）求二面角E-AC-D的大小。
（文）求三棱锥A-CDE的体积。
【答案】
（1）
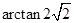（2）理
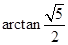，文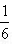
【解析】（1）过E作EF⊥AD交AD于F，则∠CEF是异面直线PA与CE的夹角（3’）
联结CF，在Rt△CEF中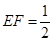
，
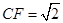
∴tan∠CEF=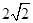
，
∴夹角大小为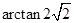（7’）
（2）（理）过F作FH⊥AC于H，则∠EHF是二面角E-AC-D的平面角（10’）
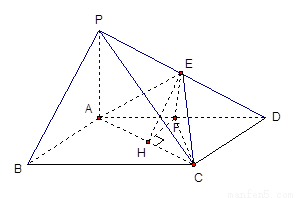HF=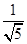
，tan ∠EHF=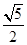
∴二面角E-AC-D的大小为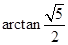（14’）
注：如构造坐标系，向量解法相应给分
（文）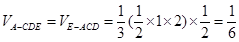
（14’）
练习册系列答案
相关题目
和梯形
所在平面互相垂直，
，
，
，
．
平面
；
的长为何值时，二面角
的大小为
？
如图，
分别是正方体
的
的中点．
//平面
；
平面
中,底面ABCD是矩形，PA⊥平面ABCD，PA=AB=1，BC=2，E为PD
的中点
