题目内容
已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直 线)行驶.甲车、
乙车的速度曲线分别为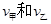 (如右图所示).那么对于图中给定的
(如右图所示).那么对于图中给定的 ,下列判断中一
,下列判断中一
定正确的是( )
乙车的速度曲线分别为
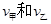 (如右图所示).那么对于图中给定的
(如右图所示).那么对于图中给定的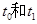 ,下列判断中一
,下列判断中一定正确的是( )

A.在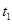 时刻,甲车在乙车前面 时刻,甲车在乙车前面 | B.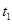 时刻后,甲车在乙车后面 时刻后,甲车在乙车后面 |
C.在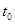 时刻,两车的位置相同 时刻,两车的位置相同 | D.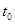 时刻后,乙车在甲车前面 时刻后,乙车在甲车前面 |
A
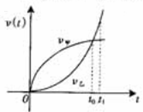
分析:利用定积分求面积的方法可知t0时刻前甲走的路程大于乙走的路程,则在t0时刻甲在乙的前面;又因为在t1时刻前利用定积分求面积的方法得到甲走的路程大于乙走的路程,甲在乙的前面;同时在t0时刻甲乙两车的速度一样,但是路程不一样.最后得到A正确,B、C、D错误.
解答:
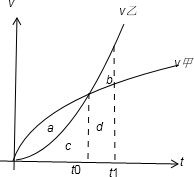
解:当时间为t0时,利用定积分得到甲走过的路程=
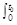 v甲dt=a+c,乙走过的路程=
v甲dt=a+c,乙走过的路程=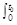 v乙dt=c;
v乙dt=c;当时间为t1时,利用定积分得到甲走过的路程=
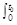 v甲dt=a+c+d,而乙走过的路程=
v甲dt=a+c+d,而乙走过的路程=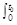 v乙dt=c+d+b;
v乙dt=c+d+b;从图象上可知a>b,所以在t1时刻,a+c+d>c+d+b即甲的路程大于乙的路程,A正确;t1时刻后,甲车走过的路程逐渐小于乙走过的路程,甲车不一定在乙车后面,所以B错;在t0时刻,甲乙走过的路程不一样,两车的位置不相同,C错;t0时刻后,t1时刻时,甲走过的路程大于乙走过的路程,所以D错.
故答案为A
点评:考查学生利用定积分求图形面积的能力,以及会观察函数图象并提取有价值数学信息的能力,数形结合的数学思想的运用能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
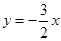
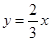
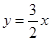
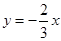
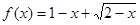 的值域为( )
的值域为( )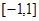
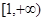
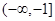
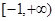

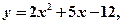
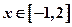 的最大值和最小值分别是
的最大值和最小值分别是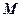 和
和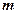 ,则
,则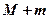
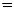
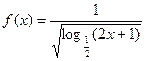 ,则
,则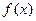 的定义域为( )
的定义域为( )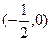
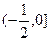
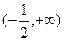
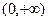
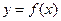 的图象关于直线
的图象关于直线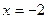 对称,当
对称,当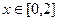 时,
时,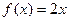 ,
, 则
则 = .
= .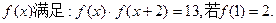 则
则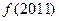 = .
= .