题目内容
22、已知a是给定的实常数，设函数f（x）=（x-a）2（x+b）e2，b∈R，x=a是f（x）的一个极大值点，求b的取值范围．
分析：先求出函数f（x）的导函数f′（x）=ex（x-a）[x2+（3-a+b）x+2b-ab-a]，令g（x）=x2+（3-a+b）x+2b-ab-a，讨论g（x）=0的两个实根x1，x2是否为a，从而确定x=a是否是f（x）的一个极大值点，建立不等关系即可求出b的范围．
解答：解：f′（x）=ex（x-a）[x2+（3-a+b）x+2b-ab-a]，
令g（x）=x2+（3-a+b）x+2b-ab-a，
则△=（3-a+b）2-4（2b-ab-a）=（a+b-1）2+8＞0，
于是，假设x1，x2是g（x）=0的两个实根，且x1＜x2．
（1）当x1=a或x2=a时，则x=a不是f（x）的极值点，此时不合题意．
（2）当x1≠a且x2≠a时，由于x=a是f（x）的极大值点，故x1＜a＜x2．
即g（a）＜0
即a2+（3-a+b）a+2b-ab-a＜0
所以b＜-a
所以b的取值范围是：（-∞，-a）
令g（x）=x2+（3-a+b）x+2b-ab-a，
则△=（3-a+b）2-4（2b-ab-a）=（a+b-1）2+8＞0，
于是，假设x1，x2是g（x）=0的两个实根，且x1＜x2．
（1）当x1=a或x2=a时，则x=a不是f（x）的极值点，此时不合题意．
（2）当x1≠a且x2≠a时，由于x=a是f（x）的极大值点，故x1＜a＜x2．
即g（a）＜0
即a2+（3-a+b）a+2b-ab-a＜0
所以b＜-a
所以b的取值范围是：（-∞，-a）
点评：本题主要考查函数极值的概念、导数运算法则、导数应用等基础知识，同时考查推理论证能力、分类讨论等综合解题能力和创新意识．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
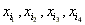(其中{i1，i2，i3，i4}={1，2，3，4})依次成等差数列？若存在，求所有的b及相应的x4；若不存在，说明理由．