题目内容
有一块边长为36的正三角形铁皮,从它的三个角剪下三个全等的四边形后做成一个无盖的正三棱柱容器,如左下图示,则这个容器的最大容积是( )
| A.288 | B.292 | C.864 | D.876 |
C
解析试题分析:根据题意,由于铁皮是边长为36的正三角形铁皮,那么从三个角剪下三个全等的四边形后做成一个无盖的正三棱柱容器,可知箱高为 ,箱子的容积为
,箱子的容积为 ,然后求解导数可知
,然后求解导数可知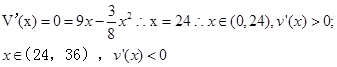
故可知函数在x=24A时取得最大值为864,故选C
考点:棱柱的体积, 导数法求最值
点评:本题考查的知识点是棱柱的体积,导数法求最值,其中根据已知求出容积V(x)的解析式,是解答的关键

练习册系列答案
相关题目
若方程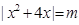 有实数根,则所有实数根的和可能为
有实数根,则所有实数根的和可能为
| A.-2,-4,-6 | B.-4,-5,-6 | C.-3,-4,-5 | D.-4,-6,-8 |
碳 的半衰期为5730年,那么碳
的半衰期为5730年,那么碳 的年衰变率为( )
的年衰变率为( )
A. | B. | C. | D. |
函数 的单调减区间为 ( )
的单调减区间为 ( )
A. | B.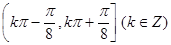 |
C. | D. |
已知函数y=4x-3×2x+3,当其值域为[1,7]时,则变量x的取值范围是
| A.[2,4] | B.(-∞,0] |
| C.(0,1]∪[2,4] | D.(-∞,0]∪[1,2] |
已知 ,实数a、b、c满足
,实数a、b、c满足 <0,且0<a<b<c,若实数
<0,且0<a<b<c,若实数 是函数
是函数 的一个零点,那么下列不等式中,不可能成立的是 ( )
的一个零点,那么下列不等式中,不可能成立的是 ( )
A. <a <a | B. >b >b | C. <c <c | D. >c >c |
函数f(x)=x2-3x+2的零点是( )
A. 或 或 | B. 或 或 |
| C.1或2 | D.-1或-2 |
 ,则
,则
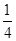 C.-4 D-
C.-4 D- 是以
是以 为周期的偶函数,当
为周期的偶函数,当 时,
时, .若关于
.若关于 的方程
的方程 (
( )在区间
)在区间 内有四个不同的实根,则
内有四个不同的实根,则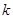 的取值范围是
的取值范围是


