题目内容
有三个推断:
(1)∵x≠0,∴x+
≥2,∴x+
的最小值为2;
(2)∵x2+1≥2x(x=1时取等号)∴x2+1的最小值为2;
(3)∵4x-x2=x(4-x)≤[
]2=4,∴4x-x2的最大值为4.
以上三个推断中正确的个数为( )
(1)∵x≠0,∴x+
| 1 |
| x |
| 1 |
| x |
(2)∵x2+1≥2x(x=1时取等号)∴x2+1的最小值为2;
(3)∵4x-x2=x(4-x)≤[
| x+(4-x) |
| 2 |
以上三个推断中正确的个数为( )
分析:(1)∵x≠0,∴x+
≥2,或x+
≤-2(2)而x=0时函数x2+1=1<2,(3)由ab≤(
)2可知推断:4x-x2=x(4-x)≤[
]2=4
| 1 |
| x |
| 1 |
| x |
| a+b |
| 2 |
| x+(4-x) |
| 2 |
解答:解(1)∵x≠0,∴x+
≥2,或x+
≤-2,错误
(2)∵x2+1≥2x(x=1时取等号)∴x2+1的最小值为2;而x=0时函数值1<2,错误
(3)由ab≤(
)2可知推断:∵4x-x2=x(4-x)≤[
]2=4,∴4x-x2的最大值为4.正确
故选:A
| 1 |
| x |
| 1 |
| x |
(2)∵x2+1≥2x(x=1时取等号)∴x2+1的最小值为2;而x=0时函数值1<2,错误
(3)由ab≤(
| a+b |
| 2 |
| x+(4-x) |
| 2 |
故选:A
点评:本题主要考查了基本不等式求解函数的最值时条件的判断:要注意检验一正,二定(和或积为定值),三相等(等号成立的条件要给以保证)

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
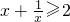 ,∴
,∴ 的最小值为2;
的最小值为2;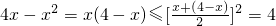 ,∴4x-x2的最大值为4.
,∴4x-x2的最大值为4.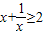 ,∴
,∴ 的最小值为2;
的最小值为2;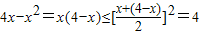 ,∴4x-x2的最大值为4.
,∴4x-x2的最大值为4.