题目内容
 (2006•朝阳区三模)已知:在正三棱柱ABC-A1B1C1中,AB=a,AA1=2a,D、E分别是侧棱BB1和AC1的中点.
(2006•朝阳区三模)已知:在正三棱柱ABC-A1B1C1中,AB=a,AA1=2a,D、E分别是侧棱BB1和AC1的中点.(Ⅰ)求异面直线AD与A1C1所成角的余弦值;
(Ⅱ)求证:ED⊥平面ACC1A1;
(Ⅲ)求平面ADC1与平面ABC所成二面角的大小.
分析:(Ⅰ)正三棱柱中AC∥A1C1,∠CAD是异面直线AD与A1C1所成的角.在△ACD中求解.
(Ⅱ)通过证明ED⊥AC.ED⊥AC1.证出ED⊥平面ACC1A1.(或证ED∥GB,GB⊥平面ACC1A1得到ED⊥平面ACC1A1.)
(Ⅲ)C1D,CB共面,则C1D,CB必相交,设交点为F,连结AF.则平面ADC1与平面ABC所成二面角是C-AF-C1.
∠C1AC是所求二面角的平面角.在△C1AC中求解.
(Ⅱ)通过证明ED⊥AC.ED⊥AC1.证出ED⊥平面ACC1A1.(或证ED∥GB,GB⊥平面ACC1A1得到ED⊥平面ACC1A1.)
(Ⅲ)C1D,CB共面,则C1D,CB必相交,设交点为F,连结AF.则平面ADC1与平面ABC所成二面角是C-AF-C1.
∠C1AC是所求二面角的平面角.在△C1AC中求解.
解答:解:(Ⅰ)∵正三棱柱中AC∥A1C1,
∴∠CAD是异面直线AD与A1C1所成的角.…(2分)
连结CD,易知AD=CD=
a,AC=a,
在△ACD中易求出cos∠CAD=
.
因此异面直线AD与A1C1所成的角的余弦值为
.…(4分)
(Ⅱ)证明:
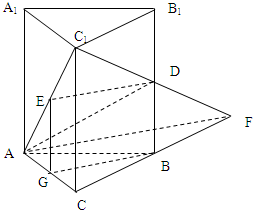
∵D是B1B的中点,
∴△C1B1D≌△ABD.
∴AD=C1D.
于是△ADC1是等腰三角形.
∵E是AC1的中点,
∴DE⊥AC1.…(6分)
设AC的中点为G,
∴EG∥C1C∥DB,EG=
C1C=DB.
∴四边形EGBD是平行四边形.
∴ED∥GB.
∵G是AC的中点,且AB=BC,
∴GB⊥AC.
∴ED⊥AC.
∵AC∩AC1=A,
∴ED⊥平面ACC1A1.…(8分)
(或证ED∥GB,GB⊥平面ACC1A1得到ED⊥平面ACC1A1.)
(Ⅲ)解:∵C1D,CB共面,
故C1D,CB必相交,设交点为F,连结AF.
∴平面ADC1与平面ABC所成二面角是C-AF-C1.…(10分)
∵DB=
C1C,DB∥C1C,
∴B是CF的中点.
∴AC=CB=BF=a.
在△ACF中,由余弦定理可求出AF=
a.
∴易判断出△ACF是直角三角形,即AC⊥AF.
∵C1C⊥面ACF,
∴AC1⊥AF.
∴∠C1AC是所求二面角的平面角.…(12分)
∵tan∠C1AC=
=2,
∴平面ADC1与平面ABC所成二面角的大小是arctan2(或arccos
).…(13分)
∴∠CAD是异面直线AD与A1C1所成的角.…(2分)
连结CD,易知AD=CD=
| 2 |
在△ACD中易求出cos∠CAD=
| ||
| 4 |
因此异面直线AD与A1C1所成的角的余弦值为
| ||
| 4 |
(Ⅱ)证明:

∵D是B1B的中点,
∴△C1B1D≌△ABD.
∴AD=C1D.
于是△ADC1是等腰三角形.
∵E是AC1的中点,
∴DE⊥AC1.…(6分)
设AC的中点为G,
∴EG∥C1C∥DB,EG=
| 1 |
| 2 |
∴四边形EGBD是平行四边形.
∴ED∥GB.
∵G是AC的中点,且AB=BC,
∴GB⊥AC.
∴ED⊥AC.
∵AC∩AC1=A,
∴ED⊥平面ACC1A1.…(8分)
(或证ED∥GB,GB⊥平面ACC1A1得到ED⊥平面ACC1A1.)
(Ⅲ)解:∵C1D,CB共面,
故C1D,CB必相交,设交点为F,连结AF.
∴平面ADC1与平面ABC所成二面角是C-AF-C1.…(10分)
∵DB=
| 1 |
| 2 |
∴B是CF的中点.
∴AC=CB=BF=a.
在△ACF中,由余弦定理可求出AF=
| 3 |
∴易判断出△ACF是直角三角形,即AC⊥AF.
∵C1C⊥面ACF,
∴AC1⊥AF.
∴∠C1AC是所求二面角的平面角.…(12分)
∵tan∠C1AC=
| C1C |
| AC |
∴平面ADC1与平面ABC所成二面角的大小是arctan2(或arccos
| ||
| 5 |
点评:本题考查空间直线、平面位置关系的判断,空间角大小求解,考查空间想象能力、推理论证、计算、转化能力.

练习册系列答案
相关题目
 (2006•朝阳区三模)函数y=f(x)的图象如图所示,则y=f(x)的导函数y=f′(x)的图象可以是( )
(2006•朝阳区三模)函数y=f(x)的图象如图所示,则y=f(x)的导函数y=f′(x)的图象可以是( )