题目内容
【题目】数列{an}的前n项a1 , a2 , …,an(n∈N*)组成集合An={a1 , a2 , …,an},从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),例如:对于数列{2n﹣1},当n=1时,A1={1},T1=1;n=2时,A2={1,3},T1=1+3,T2=13;
(1)若集合An={1,3,5,…,2n﹣1},求当n=3时,T1 , T2 , T3的值;
(2)若集合An={1,3,7,…,2n﹣1},证明:n=k时集合Ak的Tm与n=k+1时集合Ak+1的Tm(为了以示区别,用Tm′表示)有关系式Tm′=(2k+1﹣1)Tm﹣1+Tm , 其中m,k∈N*,2≤m≤k;
(3)对于(2)中集合An . 定义Sn=T1+T2+…+Tn , 求Sn(用n表示).
【答案】
(1)解:当n=3时,A3={1,3,7},
T1=1+3+7=11,T2=1×3+1×7+3×7=31,T3=1×3×7=21
(2)证明:当n=k+1时,集合Ak+1有k+1个元素,比n=k时的集合Ak多了一个元素:ak+1=2k+1﹣1.∴对应的 ![]() 包含两个部分:(i)若
包含两个部分:(i)若 ![]() 中不含ak+1,则
中不含ak+1,则 ![]() 中的任何一项恰好为n=k时集合Ak的对应的Tm中的一项.
中的任何一项恰好为n=k时集合Ak的对应的Tm中的一项.
(ii)若 ![]() 中含ak+1的任何一项,除了ak+1,其余的m﹣1个数均来自集合Ak,这m﹣1个数的乘积恰好为集合Ak所对应的Tm﹣1中的一项.
中含ak+1的任何一项,除了ak+1,其余的m﹣1个数均来自集合Ak,这m﹣1个数的乘积恰好为集合Ak所对应的Tm﹣1中的一项.
∴有关系式Tm′=(2k+1﹣1)Tm﹣1+Tm,其中m,k∈N*,2≤m≤k
(3)解:由S1=1=21﹣1=1,S2=7=23﹣1,S3=63=26﹣1,
猜想 Sn= ![]() ﹣1.下面证明:
﹣1.下面证明:
(i)易知n=1时成立.
(ii)假设n=k时,Sn=Sk= ![]() ﹣1,
﹣1,
则n=k+1时,Sk+1=T1+T2+T3+…+Tk+1
=[T1′+(2k+1﹣1)]+[T2′+(2k+1﹣1)T1′]+[T3′+(2k+1﹣1)T2′]+…+[Tk′+(2k+1﹣1)]
(其中Ti′,i=1,2,…,k,为n=k时可能的k个数的乘积的和为Tk),
=( T1′+T2′+T3′+…+Tk′)+(2k+1﹣1)+(2k+1﹣1)( T1′+T2′+T3′+…+Tk′)
=Sk+(2k+1﹣1)+(2k+1﹣1)Sk = ![]() +(2k+1﹣1)
+(2k+1﹣1)
= ![]() ﹣1,
﹣1,
即n=k+1时,Sk+1═ ![]() ﹣1也成立,
﹣1也成立,
综合(i)(ii)知对n∈N*,Sn= ![]() ﹣1成立.
﹣1成立.
∴Sn= ![]() ﹣1
﹣1
【解析】(1)当n=3时,A3={1,3,7},由定义可得:T1 , T2 , T3的值.(2)当n=k+1时,集合Ak+1有k+1个元素,比n=k时的集合Ak多了一个元素:ak+1=2k+1﹣1.对应的 ![]() 包含两个部分:(i)若
包含两个部分:(i)若 ![]() 中不含ak+1 , 则
中不含ak+1 , 则 ![]() 中的任何一项恰好为n=k时集合Ak的对应的Tm中的一项.(ii)若
中的任何一项恰好为n=k时集合Ak的对应的Tm中的一项.(ii)若 ![]() 中含ak+1的任何一项,除了ak+1 , 其余的m﹣1个数均来自集合Ak , 这m﹣1个数的乘积恰好为集合Ak所对应的Tm﹣1中的一项.即可证明.(3)由S1=1=21﹣1=1,S2=7=23﹣1,S3=63=26﹣1,猜想 Sn=
中含ak+1的任何一项,除了ak+1 , 其余的m﹣1个数均来自集合Ak , 这m﹣1个数的乘积恰好为集合Ak所对应的Tm﹣1中的一项.即可证明.(3)由S1=1=21﹣1=1,S2=7=23﹣1,S3=63=26﹣1,猜想 Sn= ![]() ﹣1.下面利用数学归纳法证明即可.
﹣1.下面利用数学归纳法证明即可.
【考点精析】通过灵活运用数列的前n项和,掌握数列{an}的前n项和sn与通项an的关系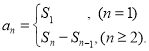 即可以解答此题.
即可以解答此题.