题目内容
【题目】某市从高二年级随机选取1000名学生,统计他们选修物理、化学、生物、政治、历史和地理六门课程(前3门为理科课程,后3门为文科课程)的情况,得到如下统计表,其中“√”表示选课,“空白”表示未选.
方案 人数 | 物理 | 化学 | 生物 | 政治 | 历史 | 地理 | |
一 | 220 | √ | √ | √ | |||
二 | 200 | √ | √ | √ | |||
三 | 180 | √ | √ | √ | |||
四 | 175 | √ | √ | √ | |||
五 | 135 | √ | √ | √ | |||
六 | 90 | √ | √ | √ | |||
(Ⅰ)在这1000名学生中,从选修物理的学生中随机选取1人,求该学生选修政治的概率;
(Ⅱ)在这1000名学生中,从选择方案一、二、三的学生中各选取2名学生,如果在这6名学生中随机选取2名,求这2名学生除选修物理以外另外两门选课中有相同科目的概率;
(Ⅲ)利用表中数据估计该市选课偏文(即选修至少两门文科课程)的学生人数多还是偏理(即选修至少两门理科课程)的学生人数多,并说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)该市选课偏理的学生人数多
;(Ⅲ)该市选课偏理的学生人数多
【解析】
(Ⅰ)根据古典概型公式求解;(Ⅱ)列出所有的情况,根据古典概型公式求解;(Ⅲ)根据样本频率估计概率判断.
(Ⅰ)设事件![]() 为“在这
为“在这![]() 名学生中,
名学生中,
从选修物理的学生中随机选取1人,该学生选修政治”.
在这![]() 名学生中,选修物理的学生人数为
名学生中,选修物理的学生人数为![]() ,
,
其中选修政治的学生人数为![]() ,所以
,所以![]() .
.
故在这![]() 名学生中,从选修物理的学生中随机选取1人,
名学生中,从选修物理的学生中随机选取1人,
该学生选修政治的概率为![]() .
.
(Ⅱ)设这六名学生分别为A1,A2,B1,B2,C1,C2,
其中A1,A2选择方案一,B1,B2选择方案二,
C1,C2选择方案三.从这6名学生中随机选取2名,
所有可能的选取方式为:
A1A2,A1B1,A1B2,A1C1,A1C2,A2B1,A2B2,A2C1,A2C2,
B1B2,B1C1,B1C2,B2C1,B2C2,C1C2,共有![]() 种选取方式.
种选取方式.
记事件![]() 为“这2名学生除选修物理以外另外两门选课中有相同科目”.
为“这2名学生除选修物理以外另外两门选课中有相同科目”.
在![]() 种选取方式中,这2名学生除选修物理以外另外两门选课中
种选取方式中,这2名学生除选修物理以外另外两门选课中
有相同科目的选取方式有A1A2,B1B2,C1C2,B1C1,B1C2,B2C1,
B2C2,A1C1,A1C2,A2C1,A2C2,共11种,因此![]() .
.
(Ⅲ)在选取的1000名学生中,
选修至少两门理科课程的人数为![]() 人, 频率为
人, 频率为![]() .
.
选修至少两门文科课程的人数为![]() 人, 频率为
人, 频率为![]() .
.
从上述数据估计该市选课偏理的学生人数多.

【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
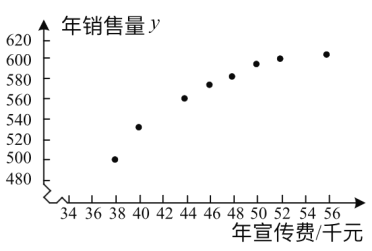
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 298.8 | 1.6 | 1469 | 108.8 |
表中![]() ,
,![]()
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)以知这种产品的年利率![]() 与
与![]() 、
、![]() 的关系为
的关系为![]() .根据(2)的结果求年宣传费
.根据(2)的结果求年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
附:对于一组数据![]() ,
,![]() ……
……![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]()