题目内容
已知四棱锥 中,底面为矩形,
中,底面为矩形, 底面
底面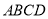 ,
, ,
,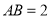 ,
, 为
为 上一点,
上一点, 为
为 的中点.
的中点.

(1)在图中作出平面 与
与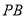 的交点
的交点 ,并指出点
,并指出点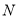 所在位置(不要求给出理由);
所在位置(不要求给出理由);
(2)求平面 将四棱锥
将四棱锥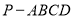 分成上下两部分的体积比.
分成上下两部分的体积比.
练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
题目内容
已知四棱锥 中,底面为矩形,
中,底面为矩形, 底面
底面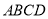 ,
, ,
,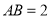 ,
, 为
为 上一点,
上一点, 为
为 的中点.
的中点.

(1)在图中作出平面 与
与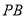 的交点
的交点 ,并指出点
,并指出点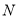 所在位置(不要求给出理由);
所在位置(不要求给出理由);
(2)求平面 将四棱锥
将四棱锥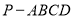 分成上下两部分的体积比.
分成上下两部分的体积比.
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案