题目内容
设函数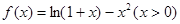 ,数列
,数列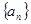 前
前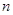 项和
项和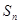 ,
,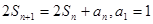 ,数列
,数列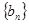 ,满足
,满足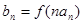 .(Ⅰ)求数列
.(Ⅰ)求数列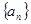 的通项公式
的通项公式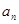 ;
;
(Ⅱ)设数列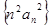 的前
的前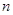 项和为
项和为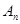 ,数列
,数列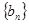 的前
的前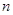 项和为
项和为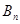 ,证明:
,证明: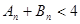 。
。
【答案】
(Ⅰ)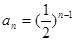 ;(Ⅱ)先放缩再求和即可得
;(Ⅱ)先放缩再求和即可得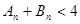 .
.
【解析】
试题分析:(Ⅰ)利用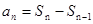 代换即可得
代换即可得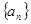 是公比为
是公比为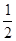 的等比数列,再利用通项公式求解即可得;(Ⅱ)先得到
的等比数列,再利用通项公式求解即可得;(Ⅱ)先得到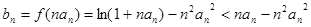 ,再用错位相减法求解即可得证.
,再用错位相减法求解即可得证.
试题解析:(Ⅰ)由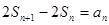 得:
得: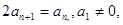
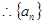 是以
是以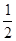 为公比的等
为公比的等
比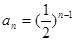 .
4分
.
4分
(Ⅱ)由
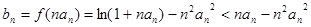 得:
得:
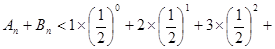 …
…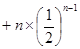 6分
6分
记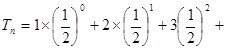 …+
…+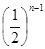 ,
,
用错位相减法可求得: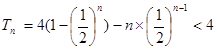
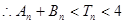 .
12分
.
12分
考点:1.数列的性质; 2.错位相减法求和.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 )是函数
)是函数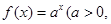 且
且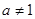 )的图象上一点,
)的图象上一点,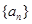 的前
的前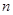 项和为
项和为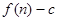 ,数列
,数列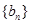
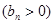 的首项为
的首项为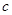 ,且前
,且前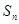 满足
满足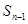 =
=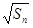 +
+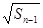 (
(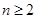 ).
).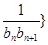 前
前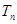 ,问
,问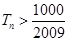 的最小正整数
的最小正整数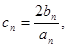 求数列
求数列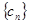 的前
的前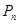
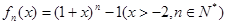 其导函数记为
其导函数记为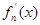 .
.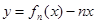 的单调递增区间;
的单调递增区间;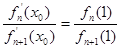 ,求证:
,求证: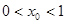 ;
;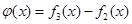 ,数列
,数列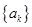 前
前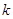 项和为
项和为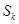 ,
, 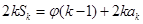 ,其中
,其中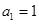 .对于给定的正整数
.对于给定的正整数 ,数列
,数列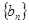 满足
满足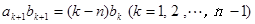 ,且
,且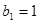 ,求
,求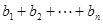 .
.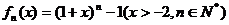 其导函数记为
其导函数记为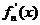 .
.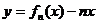 的单调递增区间;
的单调递增区间;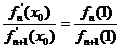 ,求证:
,求证: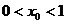 ;
;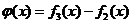 ,数列
,数列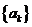 前
前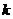 项和为
项和为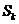 ,
,
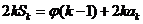 ,其中
,其中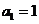 .对于给定的正整数
.对于给定的正整数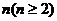 ,数列
,数列 满足
满足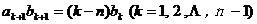 ,且
,且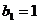 ,求
,求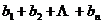 .
.