题目内容

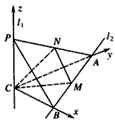
如图，l1，l2是两条互相垂直的异面直线，点P，C在直线l1上，点A， B在直线l2上，M，N分别是线段AB，AP的中点，且PC=AC=a，PA=a，
(Ⅰ)证明：PC⊥平面ABC；
(Ⅱ)设平面MNC与平面PBC所成的角为θ(0°＜θ≤90°)。现给出下列四个条件：①CM=AB；②AB=a；③CM⊥AB；④BC⊥AC。请你从中再选择两个条件以确定cosθ的值，并求解．

解：(Ⅰ)在△PAC中，∵PC=AC=a，PA=a，
∴PC2+AC2=PA2，∴PC⊥AC，
∵l1，l2是两条互相垂直的异面直线，点P，C在直线l1上，点A，B 在直线l2上，
∴PC⊥AB，
又AC∩AB=A，
∴PC⊥平面ABC．
 (Ⅱ)方案一：选择②④可确定cosθ的大小．
∵AC⊥BC，且AB=a，AC=a，
∴BC=a，以C为坐标原点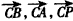，的方向为
x，y，z轴的正方向建立空直角坐标系C-xyz，
则，
又M，N分别是AB，AP的中点，
∴，
∵CA⊥平面PBC，
∴是平面PBC的一个法向量，
设平面MNC的法向量，
由，得，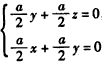
取x=1，得为平面MNC的一个法向量，
∴，
∴。
练习册系列答案
相关题目
如图，l1，l2是通过某市开发区中心0的两条南北和东西走向的道路，连接M、N两地的铁路是一段抛物线弧，它所在的抛物线关于直线L1对称．M到L1、L2的距离分别是2 km、4km，N到L1、L2的距离分别是3km、9km．
（1）建立适当的坐标系，求抛物线弧MN的方程．（2）该市拟在点0的正北方向建设一座工厂，考虑到环境问题，要求厂址到点0的距离大于5km而不超过8km，并且铁路上任意一点到工厂的距离不能小于
6
km．求此厂离点0的最近距离．（注：工厂视为一个点）
（2012•江门一模）如图是某个正方体的侧面展开图，l1、l2是两条侧面对角线，则在正方体中，l1与l2（　　）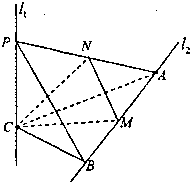
（2010•福建模拟）如图，l1、l2是两条互相垂直的异面直线，点P、C在直线l1上，点A、B在直线l2上，M、N分别是线段AB、AP的中点，且PC=AC=a，PA=
2
a．
（Ⅰ）证明：PC⊥平面ABC；
（Ⅱ）设平面MNC与平面PBC所成的角为θ（0°＜θ≤90°）．现给出下列四个条件：
①CM=
1
2
AB；②AB=
2
a；③CM⊥AB；④BC⊥AC．
请你从中再选择两个条件以确定cosθ的值，并求之．
如图，l1、l2是两条互相垂直的异面直线，点P、C在直线l1上，点A、B在直线l2上，M、N分别是线段AB、AP的中点，且PC=AC=a，．
（Ⅰ）证明：PC⊥平面ABC；
（Ⅱ）设平面MNC与平面PBC所成的角为θ（0°＜θ≤90°）．现给出下列四个条件：
①；②；③CM⊥AB；④BC⊥AC．
请你从中再选择两个条件以确定cosθ的值，并求之．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网