Question

如图，已知三棱锥O-ABC中，

OA

=

a

，

OB

=

b

，

OC

=

c

，G点为△OBC的重心，则

AG

=（　　）

• A、

  1

  3

  a

  -

  b

  +

  1

  3

  c

• B、-

  a

  +

  1

  3

  b

  +

  1

  3

  c

• C、

  1

  3

  a

  +

  1

  3

  b

  -

  c

• D、-

  a

  +

  2

  3

  b

  +

  2

  3

  c

Answer 1

分析：由于G点为△OBC的重心，可得

OG

=

2

3

OD

，

OD

=

1

2

(

OB

+

OC

)，即可得出

AG

=

AO

+

OG

．

解答：解：如图所示，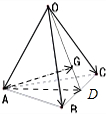
∵G点为△OBC的重心，
∴

OG

=

2

3

OD

，

OD

=

1

2

(

OB

+

OC

)，
∴

AG

=

AO

+

OG

=-

a

+

2

3

×

1

2

(

b

+

c

)=-

a

+

1

3

b

+

1

3

c

．
故选：B．

点评：本题考查了三角形的重心定理、向量的平行四边形法则和三角形法则，属于基础题．